排序算法【算法】

绯樱殇雪
2025-05-30 14:36:38
算法

文章目录

一、冒泡排序（Bubble Sort）

一种简单的排序算法，依次比较相邻元素，将较大（或较小）的元素逐渐交换到数组的末尾，直到整个数组有序。

1. 基本思想

① 从序列的第一个元素开始，依次比较相邻的两个元素。
② 如果当前元素大于后面的元素（按升序排序），则交换它们的位置。
③ 继续向后移动，重复上述比较和交换步骤，直到遍历到序列的最后一个元素。
④ 重复以上步骤，每次遍历都将待排序序列中最大的元素“冒泡”到末尾。
⑤ 经过 n − 1 n-1 次遍历后，待排序序列就会完全有序。

2. 动态演示

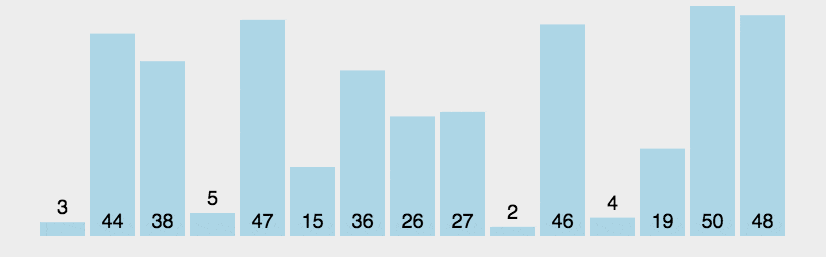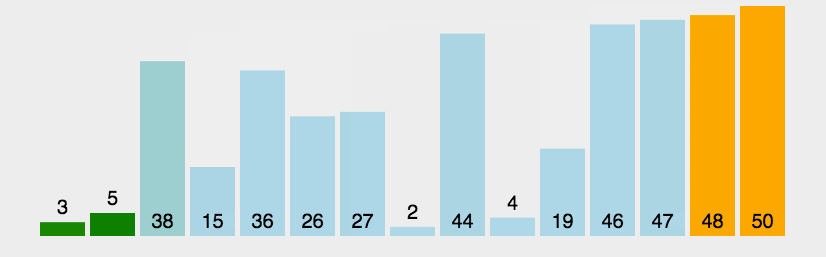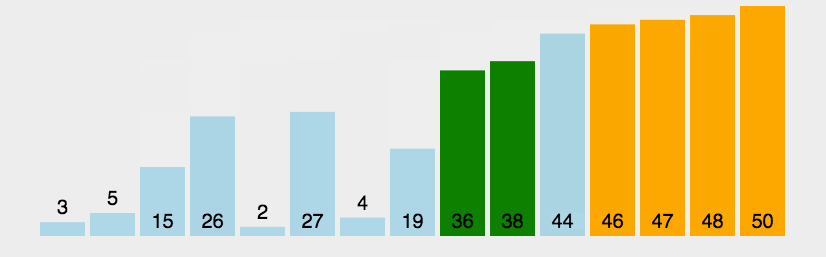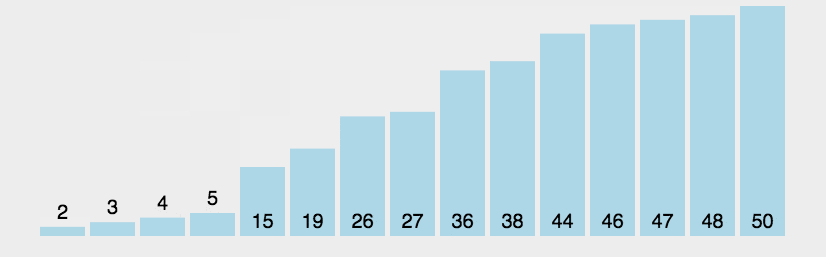
在这里插入图片描述

3. 代码实现

// C语言： #include <stdio.h> int main(void) { int array[] = {36, 48, 96, 24, 66, 50, 8, 24, 88}; // 待排序数组 int length = sizeof(array) / sizeof(array[0]); // 数组长度 for (int i = 0; i < length - 1; i++) { // 外层循环，控制比较轮数，每轮确定一个最大值 for (int j = 0; j < length - 1 - i; j++) { // 内层循环，控制比较次数，每次比较相邻两个元素大小 if (array[j] > array[j + 1]) { // 如果前一个元素比后一个元素大，交换它们的位置 int temp = array[j]; array[j] = array[j + 1]; array[j + 1] = temp; } } } for (int i = 0; i < length; i++) // 输出排序后的结果 printf("%d ", array[i]); printf("\n"); return 0; }

4. 算法性能

一种稳定的排序方法，冒泡排序思路简单，代码也简单，特别适合小数据的排序。但是，由于算法复杂度较高，在数据量大的时候不适合使用。时间复杂度为 【 O （ n 2 ）】 【O（n^2）】 ，在排序过程中仅需要一个元素的辅助空间用于元素的交换，空间复杂度为 【 O （ 1 ）】 【O（1）】 。

二、选择排序（Selection Sort）

一种简单直观的排序算法，每次从未排序的部分中选择最小（或最大）的元素，并放到已排序部分的末尾，直到整个数组有序。

1. 基本思想

① 在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
② 从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
③ 重复上一步，直到所有元素均排序完毕。

2. 动态演示

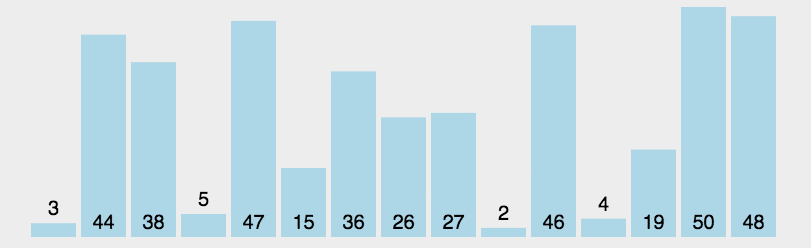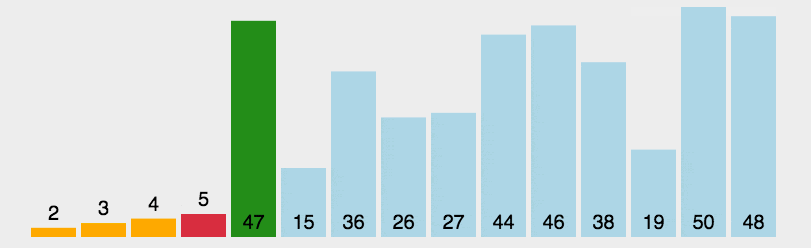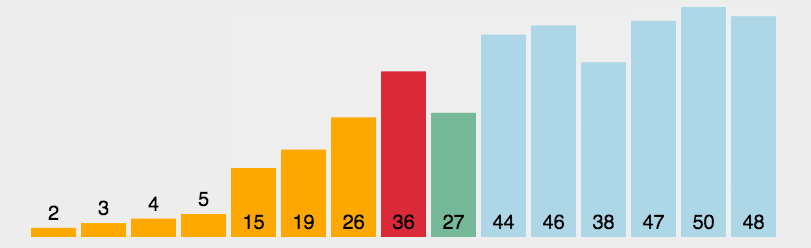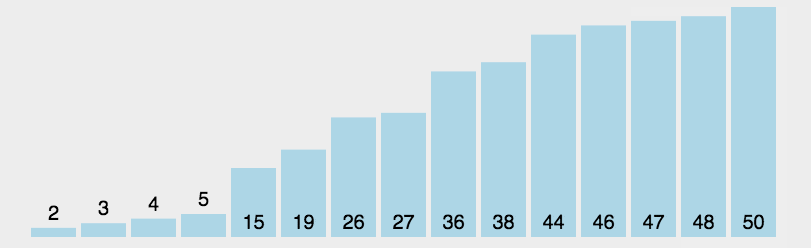
在这里插入图片描述

3. 代码实现

// C语言： #include <stdio.h> int main(void) { int array[] = {36, 48, 96, 24, 66, 50, 8, 24, 88}; // 待排序数组 int length = sizeof(array) / sizeof(array[0]); // 数组长度 for (int i = 0; i < length - 1; i++) { // 外层循环，控制比较轮数，每轮确定一个最小值 int min_index = i; // 记录最小值下标 for (int j = i + 1; j < length; j++) // 内层循环，找到当前范围内最小值的下标 if (array[j] < array[min_index]) min_index = j; int temp = array[i]; // 将最小值与当前范围内第一个元素交换位置 array[i] = array[min_index]; array[min_index] = temp; } for (int i = 0; i < length; i++) // 输出排序后的结果 printf("%d ", array[i]); printf("\n"); return 0; }

4. 算法性能

用数组实现的选择排序是不稳定的，用链表实现的选择排序是稳定的。选择排序实现也比较简单，并且由于在各种情况下复杂度波动小，因此一般是优于冒泡排序的，适用于简单数据排序，时间复杂度为 【 O （ n 2 ）】 【O（n^2）】 。

三、插入排序（Insertion Sort）

一种简单直观的排序算法，将未排序的元素逐个插入到已排序部分的正确位置，直到整个数组有序。

1. 基本思想

① 把待排序的数组分成已排序和未排序两部分，初始的时候把第一个元素认为是已排好序的。
② 从第二个元素开始，在已排好序的子数组中寻找到该元素合适的位置并插入该位置。
③ 重复上述过程直到最后一个元素被插入有序子数组中。

2. 动态演示

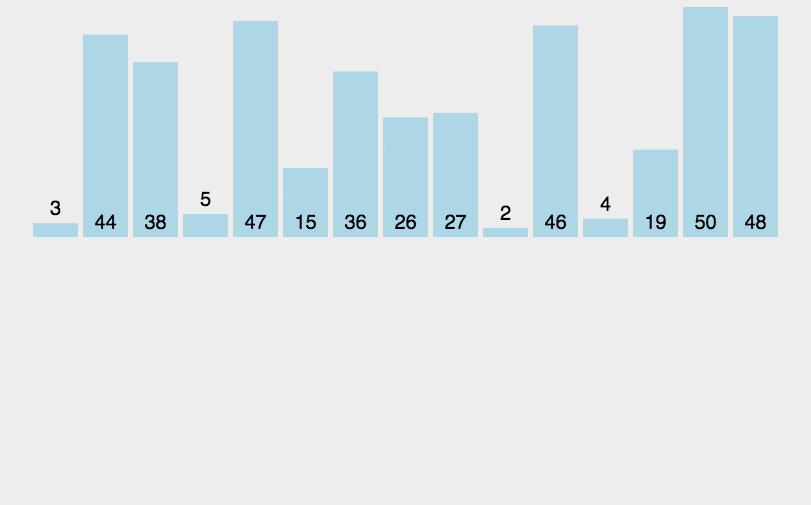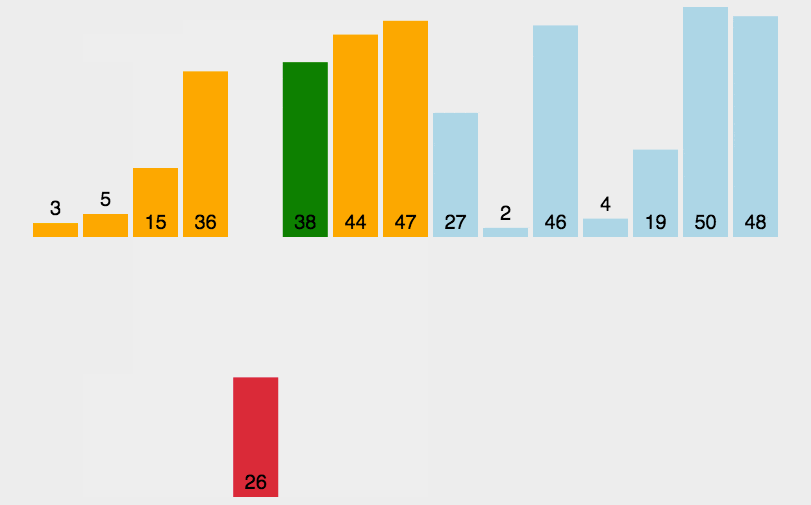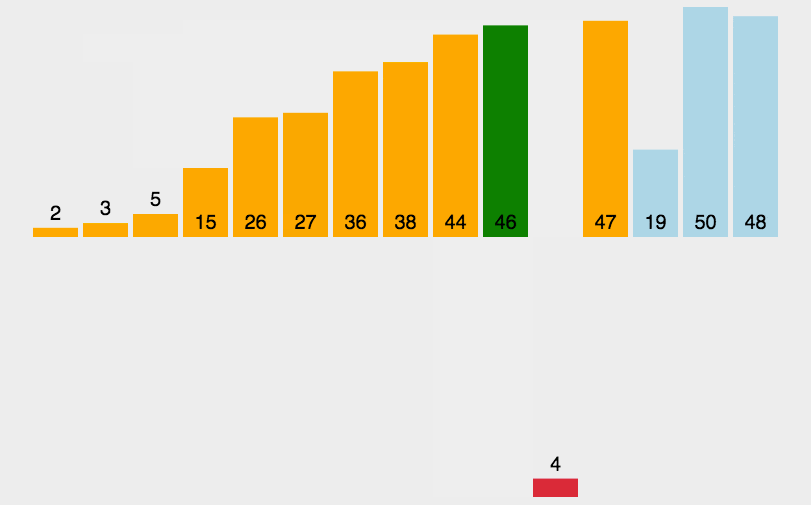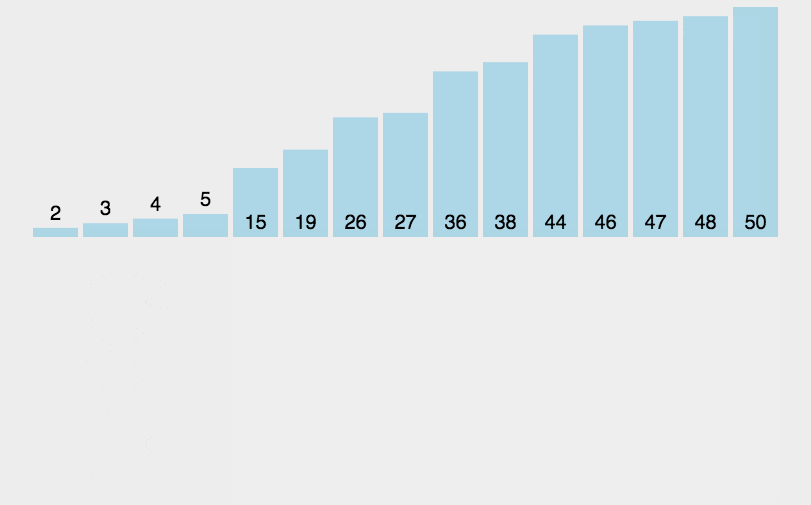
在这里插入图片描述

3. 代码实现

// C语言： #include <stdio.h> int main(void) { int array[] = {36, 48, 96, 24, 66, 50, 8, 24, 88}; // 待排序数组 int length = sizeof(array) / sizeof(array[0]); // 数组长度 for (int i = 1; i < length; i++) { // 外层循环，控制待插入元素的下标 int temp = array[i]; // 记录待插入元素的值 int j = i - 1; while (j >= 0 && array[j] > temp) { // 内层循环，将待插入元素插入到已排序部分的合适位置 array[j + 1] = array[j]; j--; } array[j + 1] = temp; } for (int i = 0; i < length; i++) // 输出排序后的结果 printf("%d ", array[i]); printf("\n"); return 0; }

4. 算法性能

一种稳定的排序方法，在数组较大的时候不适用，在数据比较少的时候，是一个不错的选择，一般做为快速排序的扩充，时间复杂度为 【 O （ n 2 ）】 【O（n^2）】 。

四、快速排序（Quick Sort）

一个知名度极高的排序算法，使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。通过选择一个基准元素，将数组分割成两部分，其中一部分小于基准元素，另一部分大于基准元素，然后对这两部分递归地进行快速排序。

1. 基本思想

① 从数列中挑出一个元素，称为 “基准”（pivot）。
② 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
③ 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

2. 动态演示

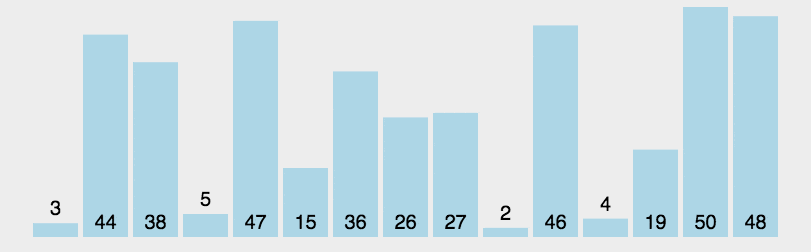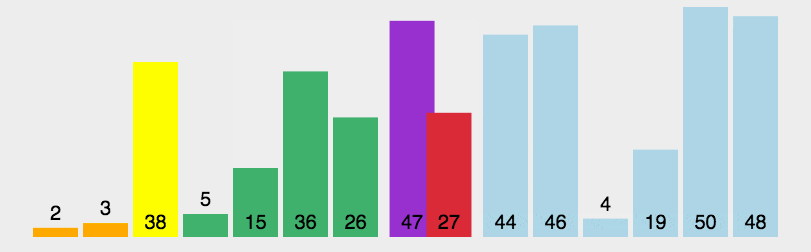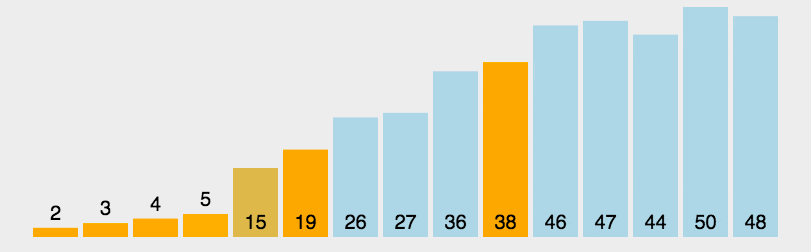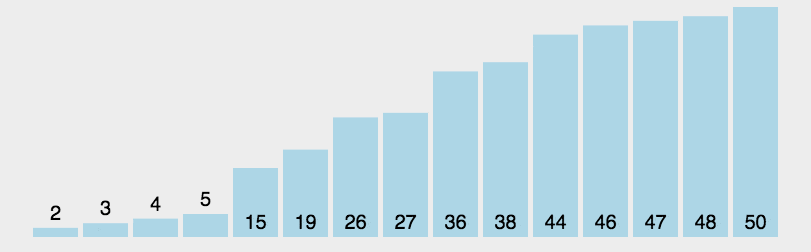
在这里插入图片描述

3. 代码实现

// C语言： #include <stdio.h> void quick_sort(int array[], int left, int right) { if (left >= right) // 递归结束条件，当left >= right时，数组已经有序 return; int i = left, j = right, pivot = array[left]; // 设定基准值为左端元素 while (i < j) { while (i < j && array[j] >= pivot) // 从右往左找第一个小于基准值的元素 j--; if (i < j) array[i++] = array[j]; while (i < j && array[i] < pivot) // 从左往右找第一个大于等于基准值的元素 i++; if (i < j) array[j--] = array[i]; } array[i] = pivot; // 将基准值插入到合适的位置 quick_sort(array, left, i - 1); // 对左半部分进行快速排序 quick_sort(array, i + 1, right); // 对右半部分进行快速排序 } int main(void) { int array[] = {36, 48, 96, 24, 66, 50, 8, 24, 88}; // 待排序数组 int length = sizeof(array) / sizeof(array[0]); // 数组长度 quick_sort(array, 0, length - 1); // 调用快速排序函数  for (int i = 0; i < length; i++) // 输出排序后的结果 printf("%d ", array[i]); printf("\n"); return 0; }

4. 算法性能

快速排序并不是稳定的，因为无法保证相等的数据按顺序被扫描到和按顺序存放。在大多数情况下都是适用的，尤其在数据量大的时候性能优越性更加明显。但是在必要的时候，需要考虑下优化以提高其在最坏情况下的性能，时间复杂度为 【 O （ n l o g n ）】 【O（n log n）】 。

五、归并排序（Merge Sort）

是建立在归并操作上的一种有效的排序算法，该算法是采用分治法的一个非常典型的应用。将数组分割成两部分，分别对这两部分进行归并排序，然后将两个有序子数组合并成一个有序数组。

1. 基本思想

  • 递归法（自上而下）
    ① 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列。
    ② 设定两个指针，最初位置分别为两个已经排序序列的起始位置。
    ③ 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置。
    ④ 重复上一步，直到某一指针到达序列尾
    ⑤ 将另一序列剩下的所有元素直接复制到合并序列尾
  • 迭代法（自下而上）
    ① 将序列每相邻两个数字进行归并操作，形成 c e i l （ n / 2 ） ceil（n/2） 个序列，排序后每个序列包含两 / 一个元素。
    ② 若此时序列数不是 1 1 个则将上述序列再次归并，形成 c e i l （ n / 4 ） ceil（n/4） 个序列，每个序列包含四 / 三个元素。
    ③ 重复上一步，直到所有元素排序完毕，即序列数为 1 1 。

2. 动态演示

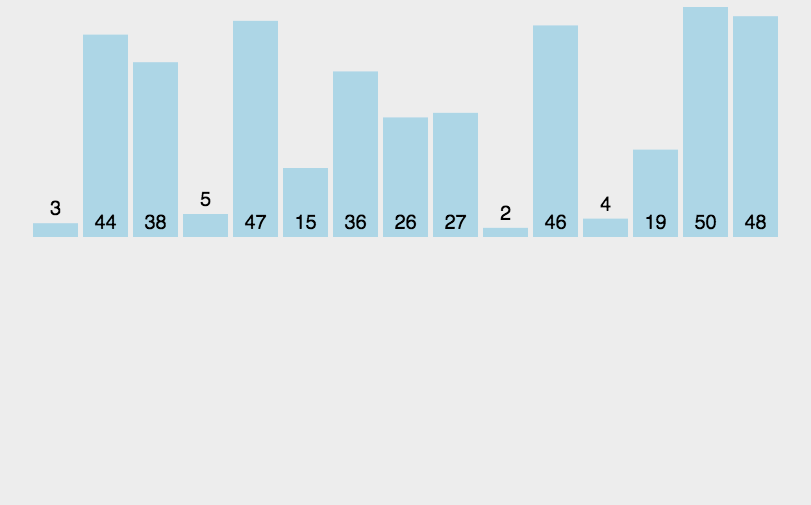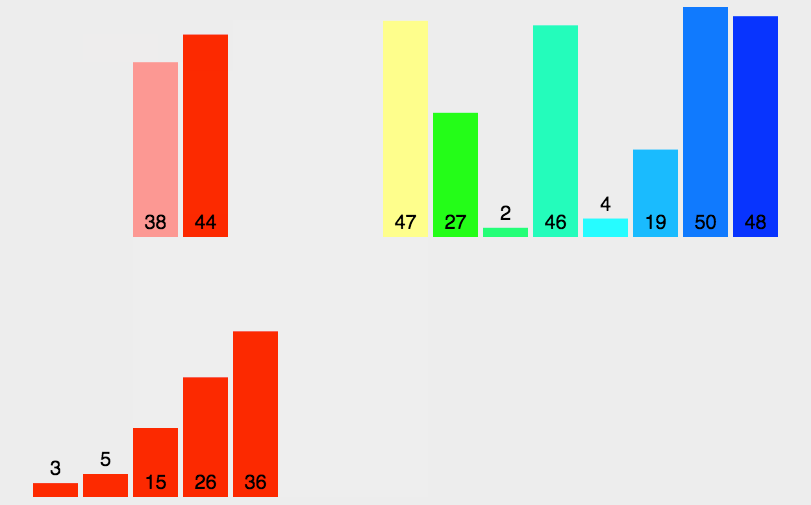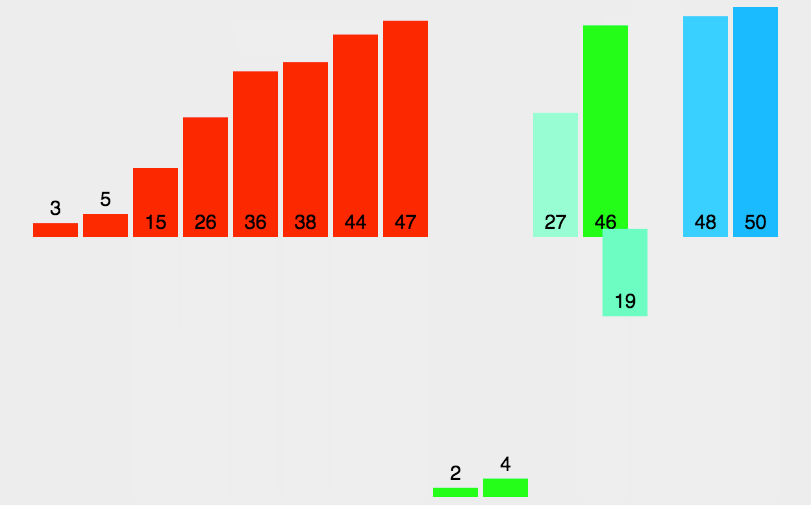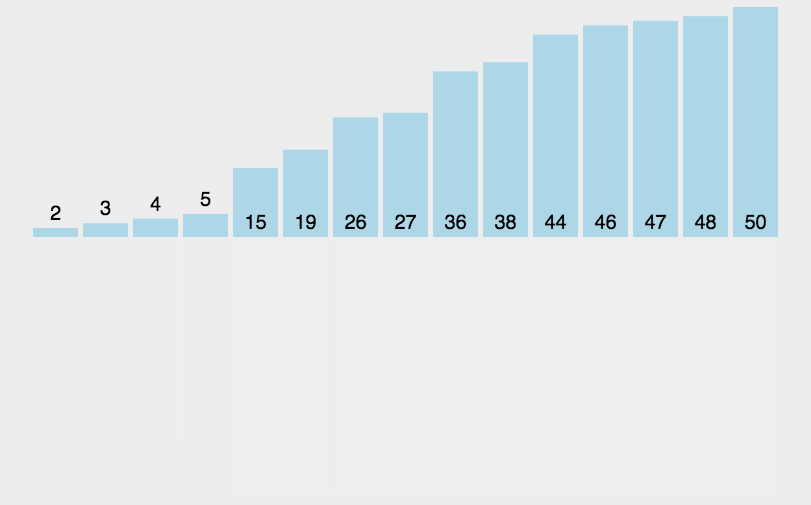
在这里插入图片描述

3. 代码实现

// C语言，递归版： #include <stdio.h> void merge(int array[], int left, int mid, int right) { // 归并函数 int n1 = mid - left + 1; // 左半部分数组的长度 int n2 = right - mid; // 右半部分数组的长度 int L[n1], R[n2]; // 临时数组 for (int i = 0; i < n1; i++) // 将数据复制到临时数组L[]和R[]中 L[i] = array[left + i]; for (int j = 0; j < n2; j++) R[j] = array[mid + 1 + j]; int i = 0, j = 0, k = left; // 归并临时数组到array[left..right] while (i < n1 && j < n2) { if (L[i] <= R[j]) { array[k] = L[i]; i++; } else { array[k] = R[j]; j++; } k++; } while (i < n1) { // 将临时数组中剩余的元素复制到array[] array[k] = L[i]; i++; k++; } while (j < n2) { array[k] = R[j]; j++; k++; } } void merge_sort(int array[], int left, int right) { // 归并排序函数 if (left < right) { int mid = left + (right - left) / 2; // 计算中间索引 merge_sort(array, left, mid); // 对左半部分进行归并排序 merge_sort(array, mid + 1, right); // 对右半部分进行归并排序 merge(array, left, mid, right); // 合并两个已排序的部分 } } int main(void) { int array[] = {36, 48, 96, 24, 66, 50, 8, 24, 88}; // 待排序数组 int length = sizeof(array) / sizeof(array[0]); // 数组长度 merge_sort(array, 0, length - 1); // 调用归并排序函数 for (int i = 0; i < length; i++) // 输出排序后的结果 printf("%d ", array[i]); printf("\n"); return 0; } // C语言，迭代版： #include <stdio.h> void merge(int array[], int left, int mid, int right) { // 归并函数 int n1 = mid - left + 1; // 左半部分数组的长度 int n2 = right - mid; // 右半部分数组的长度 int L[n1], R[n2]; // 临时数组 for (int i = 0; i < n1; i++) // 将数据复制到临时数组L[]和R[]中 L[i] = array[left + i]; for (int j = 0; j < n2; j++) R[j] = array[mid + 1 + j]; int i = 0, j = 0, k = left; // 归并临时数组到array[left..right] while (i < n1 && j < n2) { if (L[i] <= R[j]) { array[k] = L[i]; i++; } else { array[k] = R[j]; j++; } k++; } while (i < n1) { // 将临时数组中剩余的元素复制到array[] array[k] = L[i]; i++; k++; } while (j < n2) { array[k] = R[j]; j++; k++; } } void merge_sort_iterative(int array[], int length) { // 归并排序函数 int current_size; // 当前子数组大小 int left_start; // 左子数组起始索引 for (current_size = 1; current_size <= length - 1; current_size = 2 * current_size) { // 对不同大小的子数组进行合并 for (left_start = 0; left_start < length - 1; left_start += 2 * current_size) { // 每次合并的子数组对应的左起始索引 int mid = left_start + current_size - 1; // 计算中间索引 int right_end = left_start + 2 * current_size - 1; // 计算右子数组的结束索引 if (right_end > length - 1) // 确保右子数组的结束索引不超过数组长度 right_end = length - 1; merge(array, left_start, mid, right_end); // 合并两个子数组 } } } int main(void) { int array[] = {36, 48, 96, 24, 66, 50, 8, 24, 88}; // 待排序数组 int length = sizeof(array) / sizeof(array[0]); // 数组长度 merge_sort_iterative(array, length); // 调用迭代法归并排序函数 for (int i = 0; i < length; i++) // 输出排序后的结果 printf("%d ", array[i]); printf("\n"); return 0; }

4. 算法性能

一种稳定的排序方法，在数据量比较大的时候也有较为出色的表现（效率上），时间复杂度为 【 O （ n l o g n ）】 【O（n log n）】 但是，其空间复杂度为 【 O （ n ）】 【O（n）】 使得在数据量特别大的时候几乎不可接受。而且，考虑到有的机器内存本身就比较小，因此，采用归并排序一定要注意。

六、堆排序（Heap Sort）

指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。将待排序的数组构建成一个堆（大顶堆或小顶堆），然后将堆顶元素与最后一个元素交换并移出堆，重复这个过程直到堆为空，得到有序数组。

1. 基本思想

① 最大堆调整（Max-Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点。
② 创建最大堆（Build-Max-Heap）：将堆所有数据重新排序，使其成为最大堆。
③ 堆排序（Heap-Sort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算 继续进行下面的讨论前，需要注意的一个问题是：数组都是 Zero-Based，这就意味着我们的堆数据结构模型要发生改变。

2. 动态演示

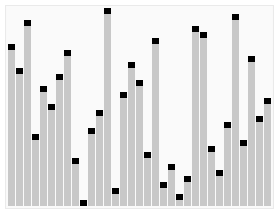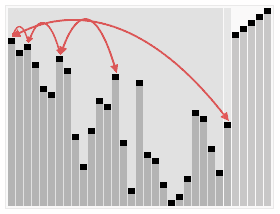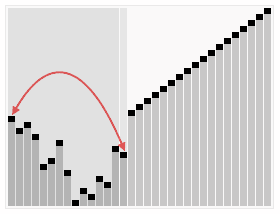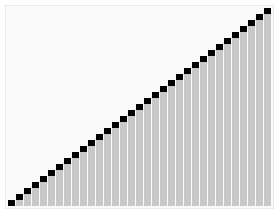
在这里插入图片描述
在这里插入图片描述

3. 代码实现

#include <stdio.h> void swap(int arr[], int i, int j) { // 交换数组中两个元素的位置 int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } void maxHeapify(int arr[], int n, int i) { // 将指定节点的值在最大堆中进行下沉操作 int largest = i; // 初始化最大值为当前节点 int left = 2 * i + 1; // 左子节点下标 int right = 2 * i + 2; // 右子节点下标 if (left < n && arr[left] > arr[largest]) largest = left; if (right < n && arr[right] > arr[largest]) largest = right; if (largest != i) { // 如果最大值不是当前节点，则将最大值上移至当前节点，并继续下沉 swap(arr, i, largest); maxHeapify(arr, n, largest); } } void heapSort(int arr[], int n) { // 使用堆排序对数组进行排序 for (int i = n / 2 - 1; i >= 0; i--) // 构建最大堆 maxHeapify(arr, n, i); for (int i = n - 1; i >= 0; i--) { // 依次将最大值交换至数组末尾并调整堆结构 swap(arr, 0, i); maxHeapify(arr, i, 0); } } int main(void) { int array[] = {36, 48, 96, 24, 66, 50, 8, 24, 88}; // 待排序数组 int length = sizeof(array) / sizeof(array[0]); // 数组长度 heapSort(arry, n); for (int i = 0; i < length; i++) // 输出排序后的结果 printf("%d ", array[i]); printf("\n"); return 0; }

4. 算法性能

一种不稳定的排序方法，在建立堆和调整堆的过程中会产生比较大的开销，在元素少的时候并不适用。但是，在元素比较多的情况下，是不错的一个选择，时间复杂度为 【 O （ n l o g n ）】 【O（n log n）】

七、希尔排序（Shell Sort）

也称递减增量排序算法，是插入排序的一种更高效的改进版本。将数组按照一定的间隔分成多个子序列，对每个子序列进行插入排序，然后逐渐减小间隔直至为1，最后进行一次完整的插入排序。

1. 基本思想

① 选择一个增量序列 t 1 ， t 2 ， … ， t k t_1，t_2，…，t_k ，其中 t i > t j ， t k = 1 t_i > t_j，t_k = 1
② 按增量序列个数 k k ，对序列进行 k k 趟排序；
③ 每趟排序，根据对应的增量 t i t_i ，将待排序列分割成若干长度为 m m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
希尔排序的增量数列可以任取，需要的唯一条件是最后一个一定为 1 1 （因为要保证按 1 1 有序）。但是，不同的数列选取会对算法的性能造成极大的影响。

2. 动态演示

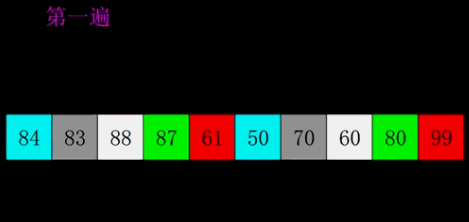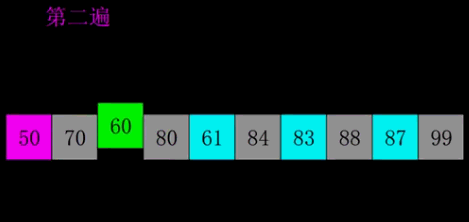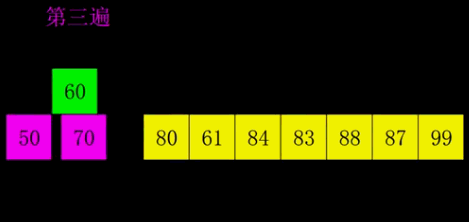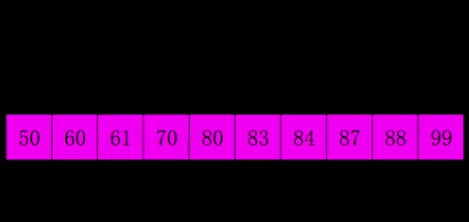
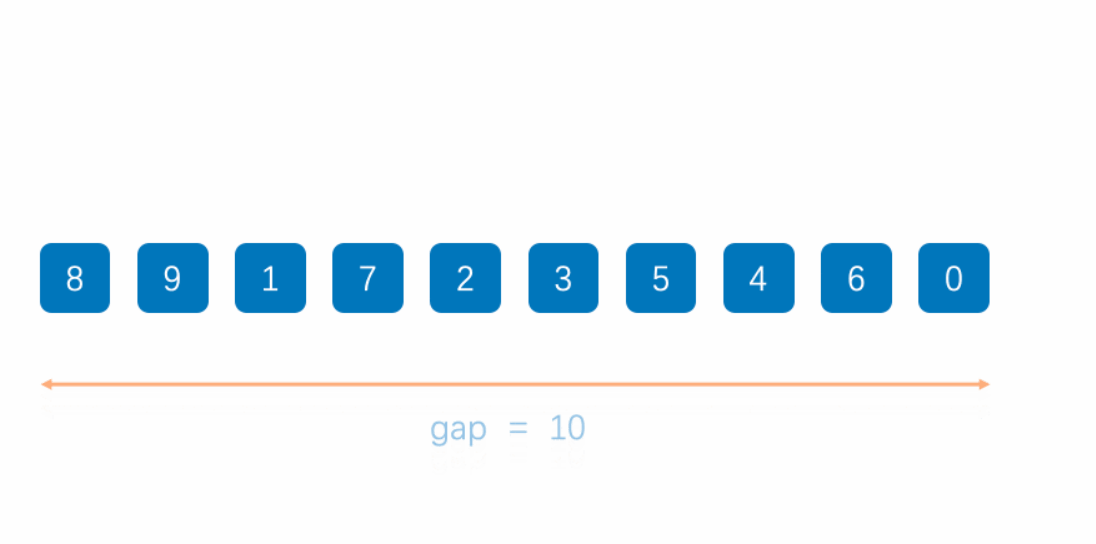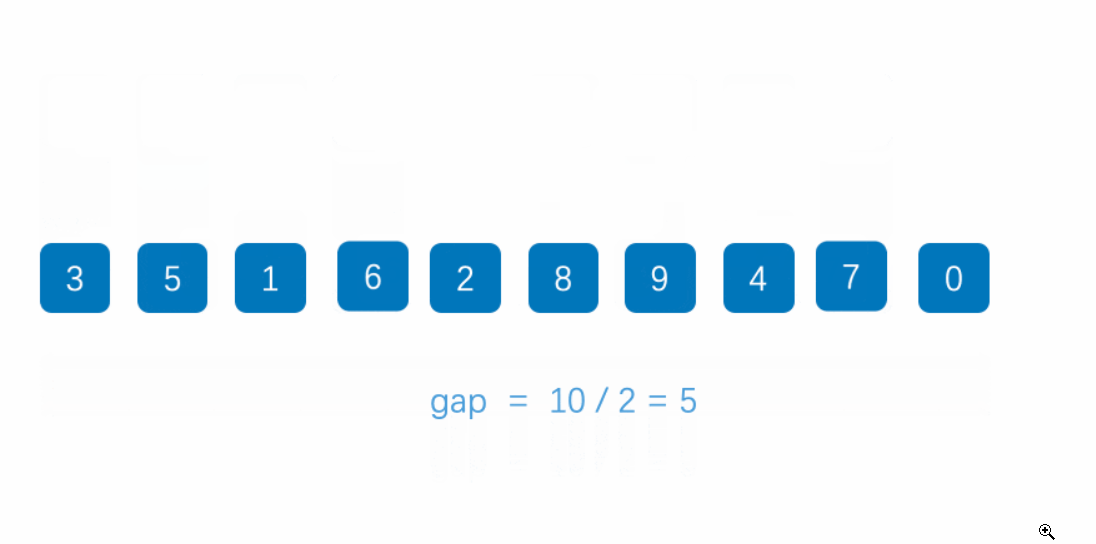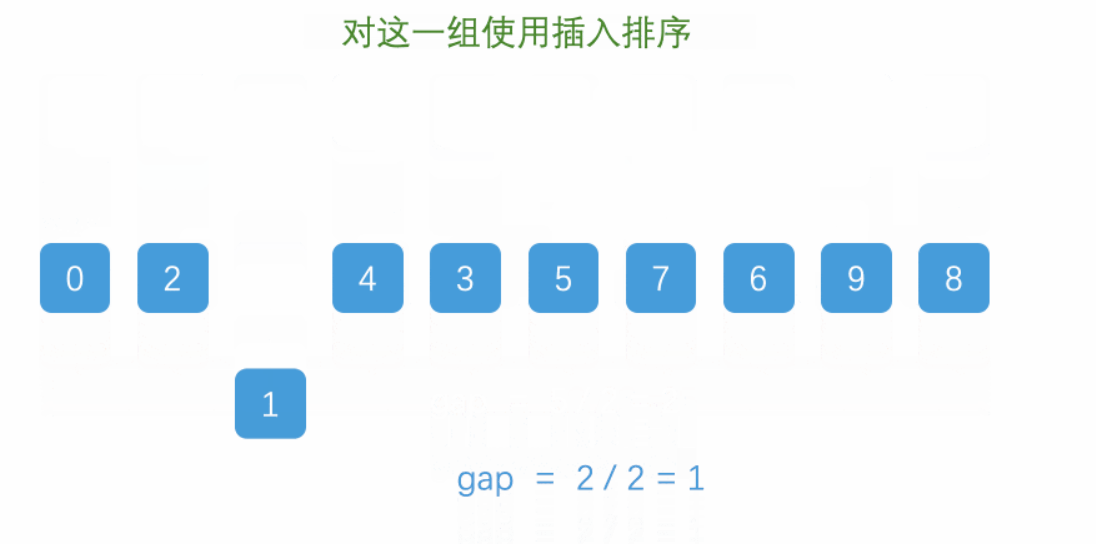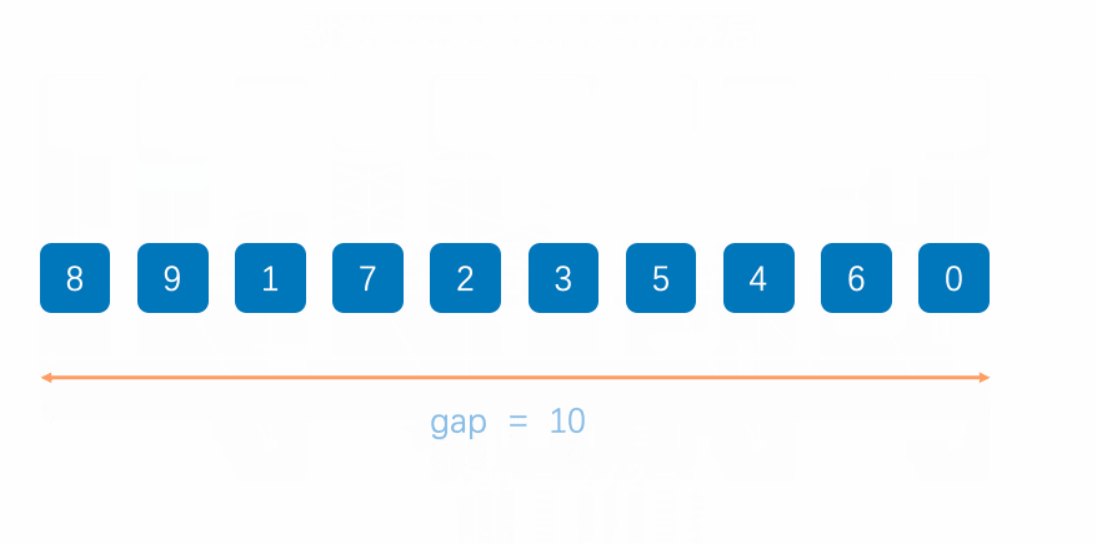
在这里插入图片描述
在这里插入图片描述

3. 代码实现

// C语言： #include <stdio.h> void shell_sort(int array[], int length) { for (int gap = length / 2; gap > 0; gap /= 2) { for (int i = gap; i < length; i++) { // 对每个子数组进行插入排序 int temp = array[i]; int j; for (j = i; j >= gap && array[j - gap] > temp; j -= gap) { // 插入排序 array[j] = array[j - gap]; } array[j] = temp; } } } int main(void) { int array[] = {36, 48, 96, 24, 66, 50, 8, 24, 88}; // 待排序数组 int length = sizeof(array) / sizeof(array[0]); // 数组长 shell_sort(array, length); // 调用希尔排序函数 for (int i = 0; i < length; i++) // 输出排序后的结果 printf("%d ", array[i]); printf("\n"); return 0; }

4. 算法性能

不是一个稳定的算法，适用于中小型规模的数据，时间复杂度为 【 O （ n l o g n ）】 【O（n log n）】 。

八、计数排序（Counting Sort）

不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。统计数组中每个元素的出现次数，然后根据元素的大小依次将元素放入正确的位置，得到有序数组。

1. 基本思想

① 找出待排序的数组中最大和最小的元素；
② 统计数组中每个值为 i i 的元素出现的次数，存入数组 C C 的第 i i 项；
③ 对所有的计数累加（从 C C 中的第一个元素开始，每一项和前一项相加）；
④ 反向填充目标数组：将每个元素i放在新数组的第 C [ i ] C[i] 项，每放一个元素就将 C [ i ] C[i] 减去 1 1 。

2. 动态演示

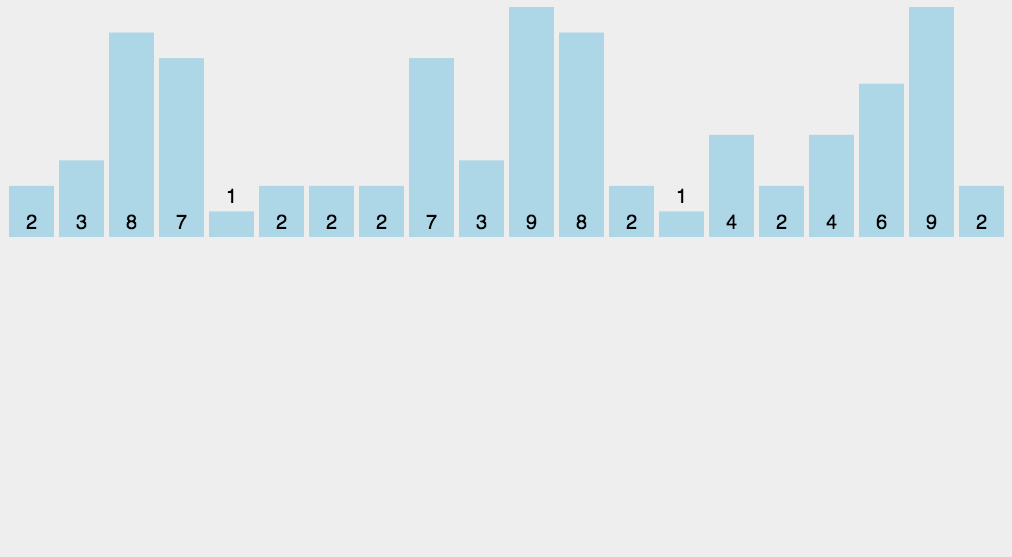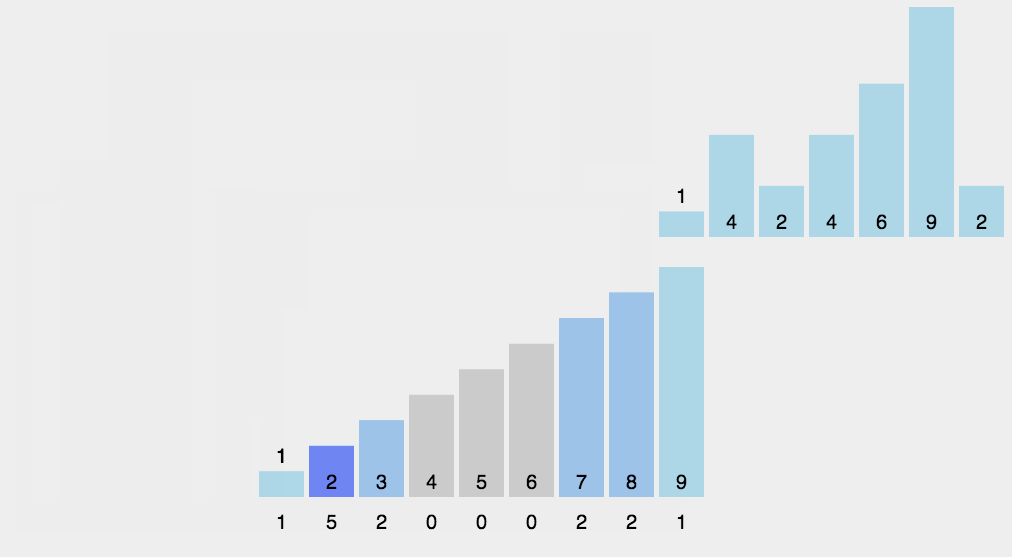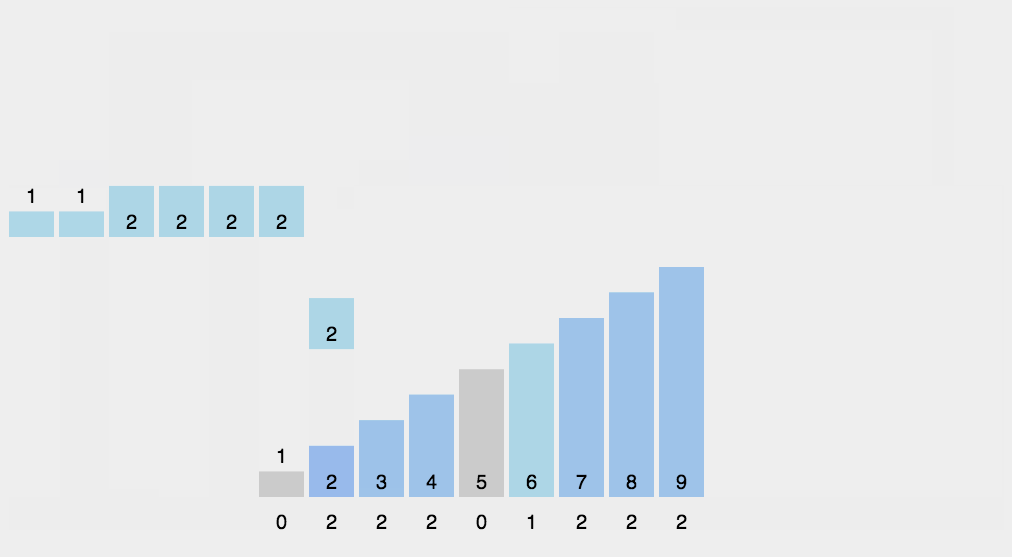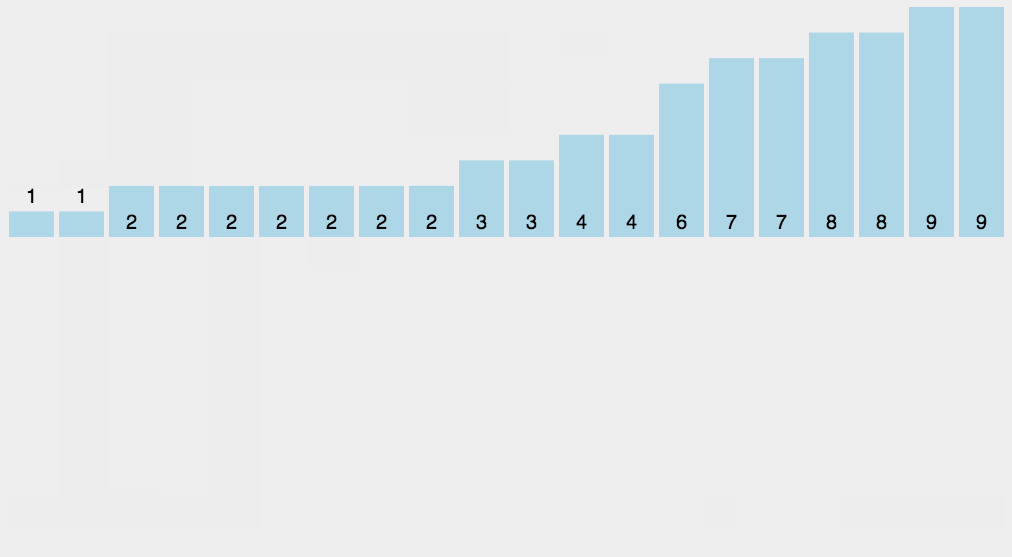
在这里插入图片描述

3. 代码实现

// C语言： #include <stdio.h> void countingSort(int arr[], int n) { // 使用计数排序对数组进行排序 int max = arr[0]; // 查找数组中的最大值 for (int i = 1; i < n; i++) if (arr[i] > max) max = arr[i]; int count[max + 1]; // 创建计数数组，用于存储每个数字出现的次数 for (int i = 0; i <= max; i++) { count[i] = 0; } for (int i = 0; i < n; i++) // 统计每个数字出现的次数 count[arr[i]]++; int output[n]; // 根据计数数组重构排序后的数组 int index = 0; for (int i = 0; i <= max; i++) { while (count[i] > 0) { output[index] = i; count[i]--; index++; } } for (int i = 0; i < n; i++) // 将排序后的数组复制回原始数组 arr[i] = output[i]; } int main(void) { int array[] = {36, 48, 96, 24, 66, 50, 8, 24, 88}; // 待排序数组 int length = sizeof(array) / sizeof(array[0]); // 数组长 countingSort(array, n); for (int i = 0; i < length; i++) // 输出排序后的结果 printf("%d ", array[i]); printf("\n"); return 0; }

4. 算法性能

是一个稳定的算法，排序目标要能够映射到整数域，其最大值最小值应当容易辨别。计数排序需要占用大量空间，它比较适用于数据比较集中的情况，时间复杂度为 【 O （ k + n ）】 【O（k + n）】 ， k k 是待排序序列中的最大值， n n 是序列的长度

九、桶排序（Bucket Sort）

是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。将待排序的元素划分到若干个有序的桶中，对每个桶内的元素进行排序，然后按照桶的顺序依次将元素取出，得到有序数组。

1. 基本思想

① 找出待排序数组中的最大值、最小值
② 使用动态数组 A r r a y L i s t ArrayList 作为桶，桶里放的元素也用 A r r a y L i s t ArrayList 存储，桶的数量为： （ m a x − m i n ） / a r r . l e n g t h + 1 （max-min）/ arr.length + 1
③ 遍历数组 a r r arr ，计算每个元素放的桶
④ 每个桶各自排序
⑤ 遍历桶数组，把排序好的元素放进输出数组

2. 动态演示

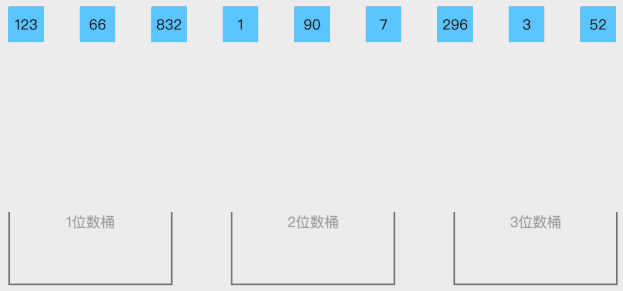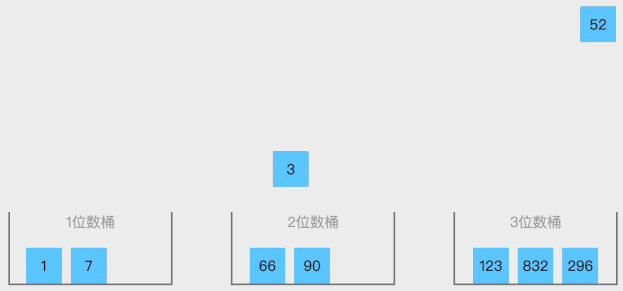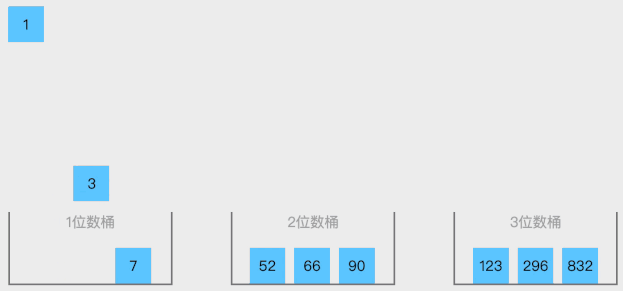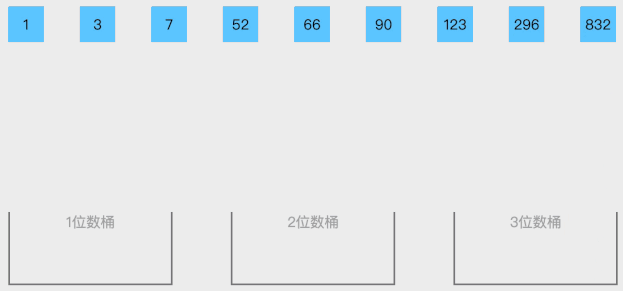
在这里插入图片描述

3. 代码实现

// C语言： #include <stdio.h> #include <stdlib.h> typedef struct bucket { // 桶结构体定义 int count; // 桶内元素数量 int* values; // 桶内元素数组 } bucket_t; void bucketSort(int arr[], int n) { // 使用桶排序对数组进行排序 bucket_t buckets[n]; // 创建桶数组 for (int i = 0; i < n; i++) { buckets[i].count = 0; buckets[i].values = NULL; } for (int i = 0; i < n; i++) { // 将每个元素分配到对应的桶中 int index = (float)n * arr[i] / (INT_MAX + 1LL); if (buckets[index].values == NULL) { buckets[index].values = malloc(sizeof(int)); } else { int* tmp = realloc(buckets[index].values, (buckets[index].count + 1) * sizeof(int)); if (tmp != NULL) { buckets[index].values = tmp; } else { printf("内存分配失败！\n"); exit(1); } } buckets[index].values[buckets[index].count++] = arr[i]; } for (int i = 0; i < n; i++) { // 对每个非空桶进行插入排序 if (buckets[i].count > 0) { for (int j = 1; j < buckets[i].count; j++) { int value = buckets[i].values[j]; int hole = j; while (hole > 0 && buckets[i].values[hole - 1] > value) { buckets[i].values[hole] = buckets[i].values[hole - 1]; hole--; } buckets[i].values[hole] = value; } } } int index = 0; // 将每个桶中的元素复制回原数组 for (int i = 0; i < n; i++) { if (buckets[i].count > 0) { for (int j = 0; j < buckets[i].count; j++) arr[index++] = buckets[i].values[j]; free(buckets[i].values); } } } int main(void) { int array[] = {6, 48, 96, 24, 66, 150, 8, 24, 288}; // 待排序数组 int length = sizeof(array) / sizeof(array[0]); // 数组长 bucketSort(arry, n); for (int i = 0; i < length; i++) // 输出排序后的结果 printf("%d ", array[i]); printf("\n"); return 0; }

4. 算法性能

是一个稳定的算法，桶排序可用于最大最小值相差较大的数据情况，但桶排序要求数据的分布必须均匀，否则可能导致数据都集中到一个桶中，时间复杂度为 【 O （ n + m ）】 【O（n + m）】 ， n n 是序列的长度， m m 是桶的数量。

十、基数排序（Radix Sort）

是桶排序的扩展，根据元素的位数进行排序，先按个位排序，再按十位排序，以此类推，直到最高位排序完成，得到有序数组。

1. 基本思想

① 取得数组中的最大数，并取得位数；
② a r r arr 为原始数组，从最低位开始取每个位组成 r a d i x radix 数组；
③ 对 r a d i x radix 进行计数排序（利用计数排序适用于小范围数的特点）；

2. 动态演示

在这里插入图片描述

3. 代码实现

#include <stdio.h> int getMax(int arr[], int n) { // 获取数组中最大的元素 int max = arr[0]; for (int i = 1; i < n; i++) if (arr[i] > max) max = arr[i]; return max; } void countingSort(int arr[], int n, int exp) { // 使用计数排序根据指定位数对数组进行排序 int output[n]; // 存储排序结果的临时数组 int count[10] = {0}; // 计数数组，用于存储每个数字出现的次数 for (int i = 0; i < n; i++) // 统计每个数字出现的次数 count[(arr[i] / exp) % 10]++; for (int i = 1; i < 10; i++) // 将count数组转换为每个数字应该在输出数组中的位置索引 count[i] += count[i - 1]; for (int i = n - 1; i >= 0; i--) { // 构建输出数组 output[count[(arr[i] / exp) % 10] - 1] = arr[i]; count[(arr[i] / exp) % 10]--; } for (int i = 0; i < n; i++) // 将输出数组复制回原始数组 arr[i] = output[i]; } void radixSort(int arr[], int n) { // 使用基数排序对数组进行排序 int max = getMax(arr, n); // 获取数组中的最大元素  for (int exp = 1; max / exp > 0; exp *= 10) // 对每个数字的每一位进行计数排序 countingSort(arr, n, exp); } int main(void) { int array[] = {36, 48, 96, 24, 66, 50, 8, 24, 88}; // 待排序数组 int length = sizeof(array) / sizeof(array[0]); // 数组长 radixSort(arr, n); for (int i = 0; i < n; i++) // 输出排序后的结果 printf("%d ", arr[i]); printf("\n"); return 0; }

4. 算法性能

是一种稳定的排序，每一轮映射和收集操作，都保持从左到右的顺序进行，如果出现相同的元素，则保持他们在原始数组中的顺序。要求较高，元素必须是整数，整数时长度 10 W 10W 以上，最大值 100 W 100W 以下效率较好，但是基数排序比其他排序好在可以适用字符串，或者其他需要根据多个条件进行排序的场景，时间复杂度为 O （ d × （ n + k ）） O（d ×（n+k）） ， n n 是待排序序列的长度， k k 是基数的范围， d d 是待排序序列的最大位数。

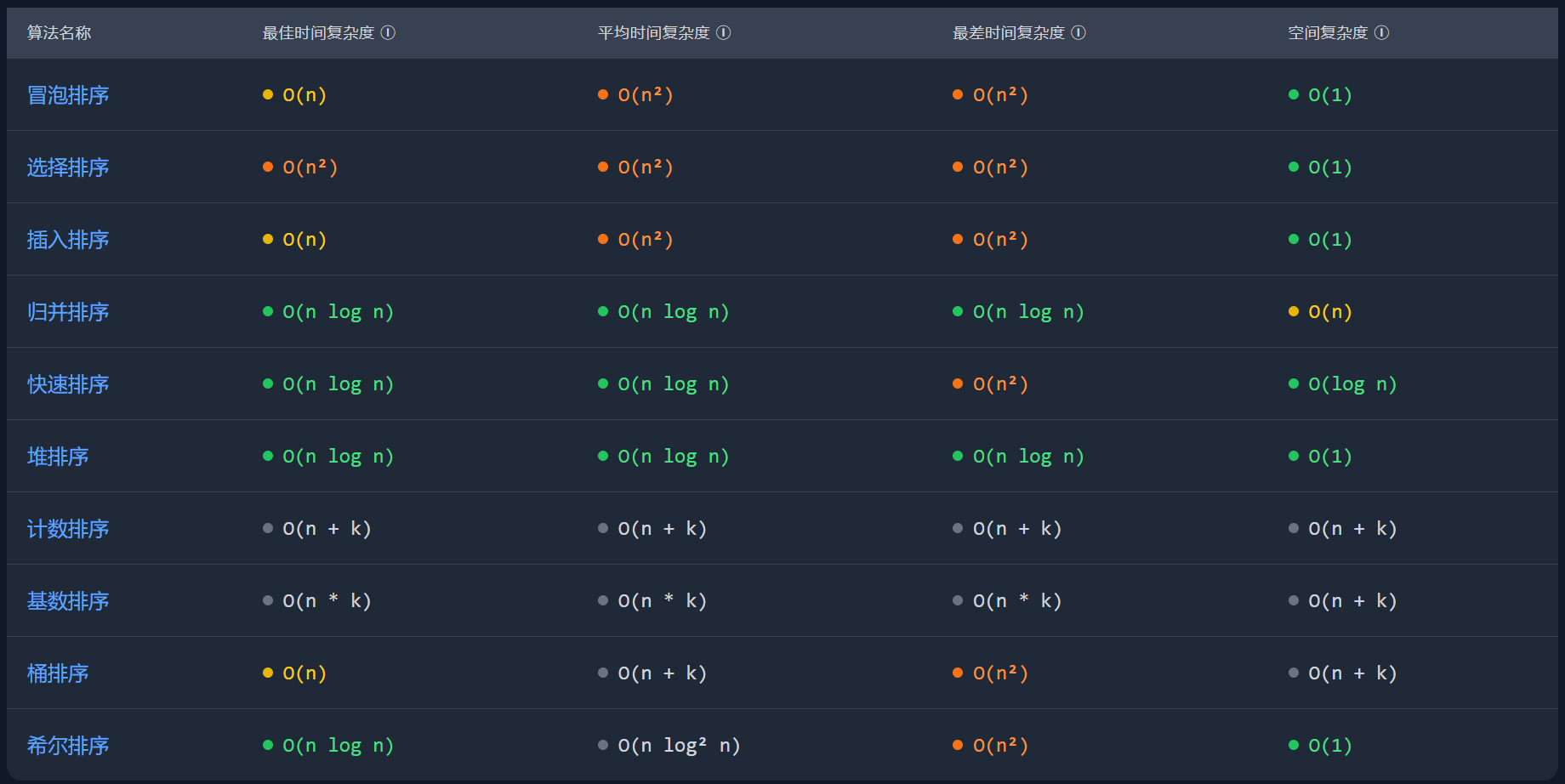
五、排序算法总结

在这里插入图片描述

本文是转载文章，点击查看原文
如有侵权，请联系 lx@jishuguiji.net 删除。