目录
1.网络流量预测的理论基础
网络流量作为一种典型的时间序列数据,具有以下特性:
周期性:受用户行为习惯影响,存在日周期、周周期和月周期等。例如,工作日白天流量高于夜间,周末流量模式与工作日不同。
趋势性:随时间推移,网络流量总体呈现增长或下降趋势,与网络规模扩张、新应用普及等因素相关。
突发性:受突发事件(如热点事件、DDoS攻击)影响,流量可能在短时间内剧烈波动。
自相关性:当前时刻流量与历史时刻流量存在显著相关性,可通过自相关函数(ACF)和偏自相关函数(PACF)量化。
非线性:复杂网络环境下,流量变化常呈现非线性特征,传统线性模型难以准确捕捉。
传统预测方法包括:
统计模型:如ARIMA、GARCH等,假设数据线性且平稳,无法处理高度非线性和非平稳的流量数据。
机器学习模型:如SVM、随机森林等,需手动提取特征,难以挖掘流量的深层时空特征。
时间序列分解法:将流量分解为趋势、周期和残差项,但对突变点和异常值敏感。
深度学习模型通过自动特征提取和非线性映射,有效克服了上述局限性。
2.深度学习LSTM模型在流量预测的应用
长短期记忆网络 (Long Short-Term Memory, LSTM) 是一种特殊的循环神经网络 (RNN),由 Hochreiter和Schmidhuber于1997年提出,旨在解决传统 RNN 的梯度消失问题,从而有效捕捉序列数据中的长期依赖关系。
2.1 LSTM基本理论
LSTM通过引入门控机制解决RNN的梯度消失问题,其核心组件包括:


LSTM通过遗忘门选择性保留长期依赖信息,适合捕捉网络流量中的长周期模式。
2.2 LSTM流量预测模型架构
基于LSTM的网络流量预测模型通常包含以下组件:

给定历史流量序列X={x1,x2,...,xT},LSTM的目标是预测未来时刻的流量值y^T+1。LSTM的预测过程可表示为:

其中yi为真实值,y^i为预测值,N为样本数。
3.基于LSTM的网络流量预测MATLAB仿真
我们编写如下的代码:
% 基于LSTM的网络流量预测
% 基于LSTM的网络流量预测
clear all;
close all;
clc;
%% 参数设置
% 数据参数
data_length = 1000; % 数据总长度
train_ratio = 0.7; % 训练集比例
val_ratio = 0.15; % 验证集比例
test_ratio = 0.15; % 测试集比例
% LSTM网络参数
numFeatures = 24; % 输入特征数
numResponses = 1; % 输出响应数
numHiddenUnits = 256; % 隐藏单元数
numTimeSteps = 24; % 时间步长
numEpochs = 100; % 训练轮数
miniBatchSize = 32; % 批处理大小
% 网络拓扑参数
numNodes = 3; % 节点数
numLinks = 5; % 链路数
linkCapacities = 100 * ones(numLinks, 1); % 链路容量
% 强化学习参数
numStates = numLinks; % 状态空间维度
numActions = numLinks; % 动作空间维度
alpha = 0.1; % 学习率
gamma = 0.9; % 折扣因子
epsilon = 0.1; % 探索率
numEpisodes = 1000; % 训练回合数
%% 生成合成网络流量数据
rng(42); % 设置随机种子,确保结果可复现
% 生成基础流量(包含趋势、周期和噪声)
time = 1:data_length;
trend = 0.01 * time';
daily_cycle = 20 * sin(2 * pi * time' / 24);
weekly_cycle = 30 * sin(2 * pi * time' / (24 * 7));
noise = 5 * randn(data_length, 1);
% 合成流量数据
traffic_data = trend + daily_cycle + weekly_cycle + noise;
% 为不同链路生成相关流量
correlation_matrix = 0.7 * ones(numLinks) + 0.3 * eye(numLinks);
traffic_data_links = zeros(data_length, numLinks);
for i = 1:numLinks
% 基础流量加随机波动
traffic_data_links(:, i) = traffic_data + 10 * randn(data_length, 1);
end
% 应用相关性
for i = 1:numLinks
for j = i+1:numLinks
% 调整流量使其具有相关性
traffic_data_links(:, j) = correlation_matrix(i, j) * traffic_data_links(:, i) + ...
sqrt(1 - correlation_matrix(i, j)^2) * traffic_data_links(:, j);
end
end
% 数据归一化
traffic_data_norm = zeros(size(traffic_data_links));
for i = 1:numLinks
traffic_data_norm(:, i) = (traffic_data_links(:, i) - min(traffic_data_links(:, i))) / ...
(max(traffic_data_links(:, i)) - min(traffic_data_links(:, i)));
end
%% 数据预处理 - 为LSTM准备序列数据
% 划分训练集、验证集和测试集
numTrainSamples = floor(data_length * train_ratio);
numValSamples = floor(data_length * val_ratio);
numTestSamples = data_length - numTrainSamples - numValSamples;
% 为每个链路训练一个LSTM模型
prediction_models = cell(numLinks, 1);
prediction_results = zeros(numTestSamples, numLinks);
for link_idx = 1:numLinks
fprintf('训练链路 %d 的LSTM模型...\n', link_idx);
% 提取当前链路的流量数据
link_data = traffic_data_norm(:, link_idx);
% 创建序列数据
X = cell(data_length - numTimeSteps, 1);
Y = zeros(data_length - numTimeSteps, 1);
for i = 1:(data_length - numTimeSteps)
X{i} = link_data(i:i+numTimeSteps-1);
Y(i) = link_data(i+numTimeSteps);
end
% 划分数据集
XTrain = X(1:numTrainSamples-numTimeSteps);
YTrain = Y(1:numTrainSamples-numTimeSteps);
XVal = X(numTrainSamples-numTimeSteps+1:numTrainSamples+numValSamples-numTimeSteps);
YVal = Y(numTrainSamples-numTimeSteps+1:numTrainSamples+numValSamples-numTimeSteps);
XTest = X(numTrainSamples+numValSamples-numTimeSteps+1:end);
YTest = Y(numTrainSamples+numValSamples-numTimeSteps+1:end);
% 创建LSTM网络
layers = [ ...
sequenceInputLayer(numFeatures)
lstmLayer(numHiddenUnits, 'OutputMode', 'last')
fullyConnectedLayer(numResponses)
regressionLayer];
if link_idx==numLinks
% 设置训练选项
options = trainingOptions('adam', ...
'MaxEpochs', numEpochs, ...
'GradientThreshold', 1, ...
'InitialLearnRate', 0.005, ...
'LearnRateSchedule', 'piecewise', ...
'LearnRateDropPeriod', 50, ...
'LearnRateDropFactor', 0.2, ...
'Plots', 'training-progress', ...
'MiniBatchSize', miniBatchSize, ...
'ValidationData', {XVal, YVal}, ...
'ValidationFrequency', 30);
else
% 设置训练选项
options = trainingOptions('adam', ...
'MaxEpochs', numEpochs, ...
'GradientThreshold', 1, ...
'InitialLearnRate', 0.005, ...
'LearnRateSchedule', 'piecewise', ...
'LearnRateDropPeriod', 50, ...
'LearnRateDropFactor', 0.2, ...
'Verbose', 0, ... % 'Plots', 'training-progress', ...
'MiniBatchSize', miniBatchSize, ...
'ValidationData', {XVal, YVal}, ...
'ValidationFrequency', 30);
end
% 训练网络
net = trainNetwork(XTrain, YTrain, layers, options);
prediction_models{link_idx} = net;
% 在测试集上评估模型
YPred = predict(net, XTest);
prediction_results(:, link_idx) = YPred;
% 计算预测误差
mse = mean((YPred - YTest).^2);
rmse = sqrt(mse);
mae = mean(abs(YPred - YTest));
fprintf('链路 %d 预测结果: MSE = %.4f, RMSE = %.4f, MAE = %.4f\n', ...
link_idx, mse, rmse, mae);
end
%% 可视化结果
% 1. 原始流量与预测流量对比
figure;
link_to_plot = 1; % 选择要绘制的链路
test_start_idx = numTrainSamples + numValSamples - numTimeSteps + 1;
test_end_idx = test_start_idx + numTestSamples - 1;
plot(time(test_start_idx:test_end_idx), traffic_data_links(test_start_idx:test_end_idx, link_to_plot), 'b-', 'LineWidth', 1.5);
hold on;
plot(time(test_start_idx:test_end_idx), prediction_results(:, link_to_plot) * ...
(max(traffic_data_links(:, link_to_plot)) - min(traffic_data_links(:, link_to_plot))) + min(traffic_data_links(:, link_to_plot)), 'r--', 'LineWidth', 1.5);
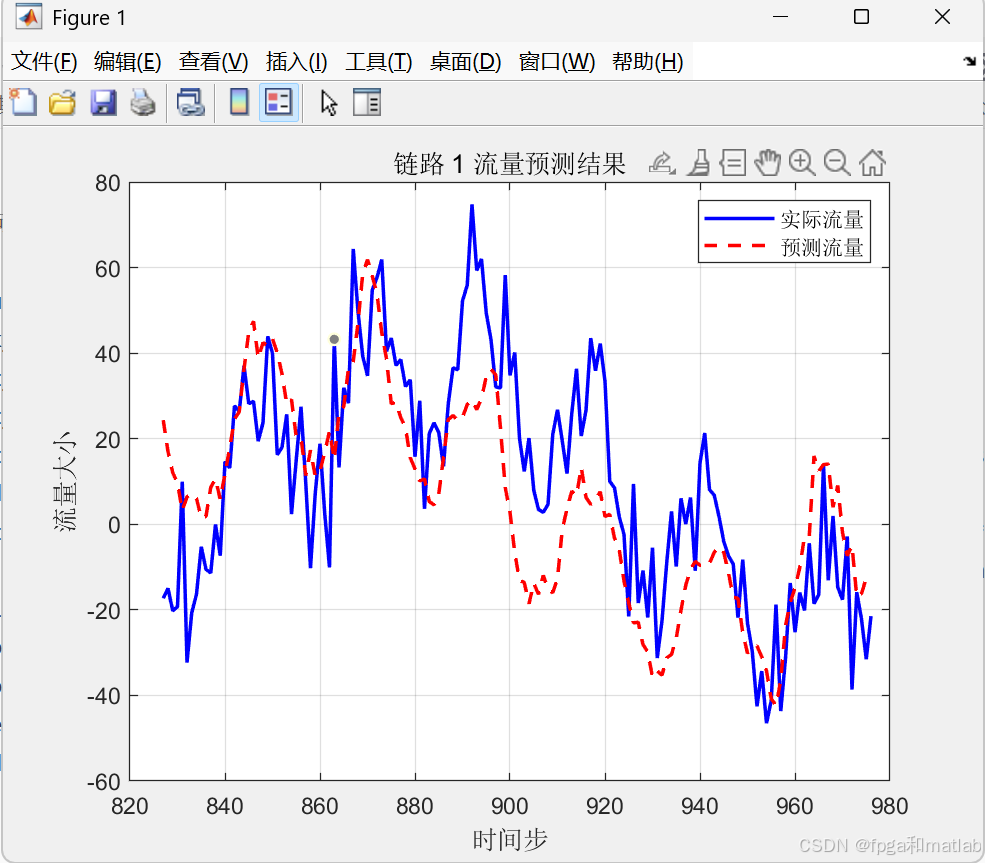
title(['链路 ', num2str(link_to_plot), ' 流量预测结果']);
xlabel('时间步');
ylabel('流量大小');
legend('实际流量', '预测流量');
grid on;
训练过程如下:
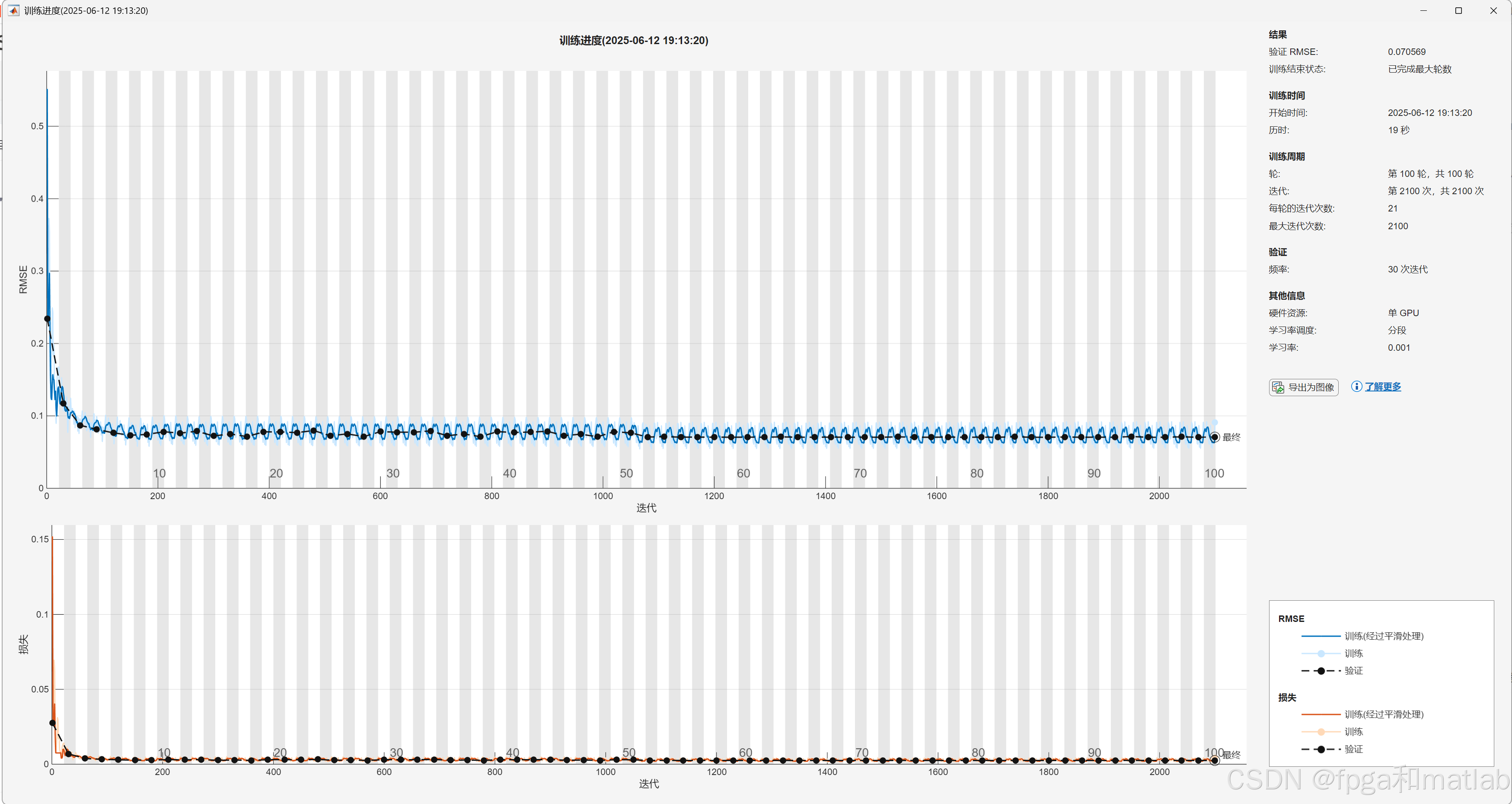
测试结果如下:
欢迎订阅FPGA/MATLAB/Simulink系列教程
