汉诺塔问题源自印度一个古老的传说,印度教的“创造之神”梵天创造世界时做了 3 根金刚石柱,其中的一根柱子上按照从小到大的顺序摞着 64 个黄金圆盘。梵天命令一个叫婆罗门的门徒将所有的圆盘移动到另一个柱子上,移动过程中必须遵守以下规则:
- 每次只能移动柱子最顶端的一个圆盘;
- 每个柱子上,小圆盘永远要位于大圆盘之上;
图 1 给您展示了包含 3 个圆盘的汉诺塔问题:
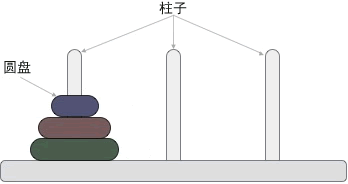
图 1 汉诺塔问题
一根柱子上摞着 3 个不同大小的圆盘,那么在不违反规则的前提下,如何将它们移动到另一个柱子上呢?图 2 给大家提供了一种实现方案:
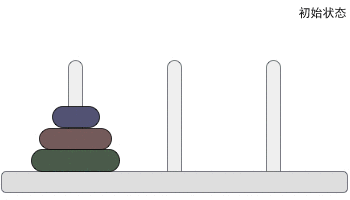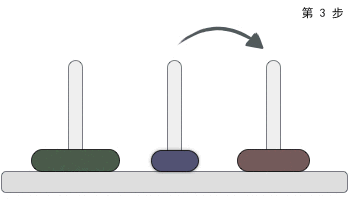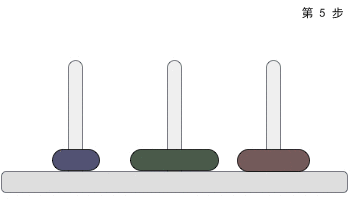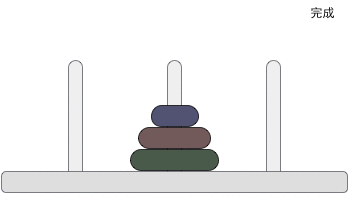
图 2 汉诺塔问题的解决方案
汉诺塔问题中,3 个圆盘至少需要移动 7 次,移动 n 的圆盘至少需要操作 2n-1 次。
在汉诺塔问题中,当圆盘个数不大于 3 时,多数人都可以轻松想到移动方案,随着圆盘数量的增多,汉诺塔问题会越来越难。也就是说,圆盘的个数直接决定了汉诺塔问题的难度。
解决汉诺塔问题,可以用分治算法,将移动多个圆盘的问题分解成多个移动少量圆盘的小问题,这些小问题很容易解决,从而可以找到整个问题的解决方案。
汉诺塔问题解决思路
为了方便讲解,我们将 3
个柱子分别命名为起始柱、目标柱和辅助柱。实际上,解决汉诺塔问题是有规律可循的:
1) 当起始柱上只有 1 个圆盘时,我们可以很轻易地将它移动到目标柱上;
2) 当起始柱上有 2 个圆盘时,移动过程如下图所示:
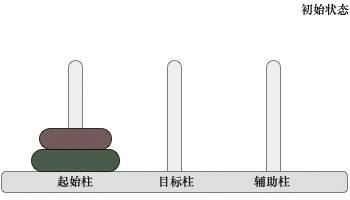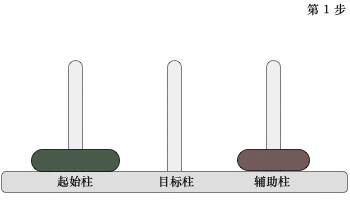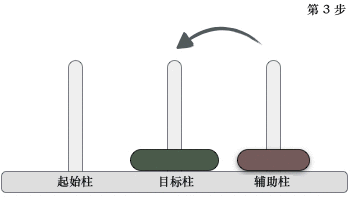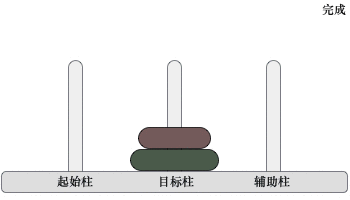
图 3 移动两个圆盘
移动过程是:先将起始柱上的 1 个圆盘移动到辅助柱上,然后将起始柱上遗留的圆盘移动到目标柱上,最后将辅助柱上的圆盘移动到目标柱上。
3) 当起始柱上有 3 个圆盘时,移动过程如图 2 所示,仔细观察会发现,移动过程和 2 个圆盘的情况类似:先将起始柱上的 2 个圆盘移动到辅助柱上,然后将起始柱上遗留的圆盘移动到目标柱上,最后将辅助柱上的圆盘移动到目标柱上。
通过分析以上 3 种情况的移动思路,可以总结出一个规律:对于 n 个圆盘的汉诺塔问题,移动圆盘的过程是:
- 将起始柱上的 n-1 个圆盘移动到辅助柱上;
- 将起始柱上遗留的 1 个圆盘移动到目标柱上;
- 将辅助柱上的所有圆盘移动到目标柱上。
由此,n 个圆盘的汉诺塔问题就简化成了 n-1 个圆盘的汉诺塔问题。按照同样的思路,n-1 个圆盘的汉诺塔问题还可以继续简化,直至简化为移动 3 个甚至更少圆盘的汉诺塔问题。
汉诺塔问题的C语言实现
如下是解决汉诺塔问题的 C 语言程序:
#include <stdio.h> void hanoi(int num, char sou, char tar,char aux) { //统计移动次数 static int i = 1; //如果圆盘数量仅有 1 个,则直接从起始柱移动到目标柱 if (num == 1) { printf("第%d次:从 %c 移动至 %c\n", i, sou, tar); i++; } else { //递归调用 hanoi() 函数,将 num-1 个圆盘从起始柱移动到辅助柱上 hanoi(num - 1, sou, aux, tar); //将起始柱上剩余的最后一个大圆盘移动到目标柱上 printf("第%d次:从 %c 移动至 %c\n", i, sou, tar); i++; //递归调用 hanoi() 函数,将辅助柱上的 num-1 圆盘移动到目标柱上 hanoi(num - 1, aux, tar, sou); } } int main() { //以移动 3 个圆盘为例,起始柱、目标柱、辅助柱分别用 A、B、C 表示 hanoi(3, 'A', 'B', 'C'); return 0; }
执行结果均为:
第1次:从 A 移动至 B
第2次:从 A 移动至 C
第3次:从 B 移动至 C
第4次:从 A 移动至 B
第5次:从 C 移动至 A
第6次:从 C 移动至 B
第7次:从 A 移动至 B

