文章目录
- 一、 算法设计与分析的基本概念
- 2. 算法设计
- 3. 算法分析
- 4. 算法的表示
- 二、 算法分析基础
- 2. 空间复杂度
- 2. 渐进符号
- 3. 递归式
- 三、 分治法
- 2. 分治法的基本思想概念
- 3. 分治法的典型实例
- 四、 动态规划法
- 2. 动态规划法的典型实例
- 五、 贪心法
- 2. 贪心法的典型实例
- 六、 回溯法
- 2. 回溯法的典型实例
- 七、 分支限界法
- 八、 概率算法
- 九、 近似算法
- 十、 数据挖掘算法
- 2. 分类
- 3. 频繁模式和关联规则挖掘
- 4. 聚类
- 十一、 智能优化算法
- 2. 人工神经网络(ANN)
- 3. 遗传算法
- 4. 模拟退火(SA)算法
- 5. 禁忌搜索(TA)算法
- 6. 蚁群算法
- 7. 粒子群优化算(PSO)
一、 算法设计与分析的基本概念
1. 算法(Algorithm)
对特定问题求解步骤的一种描述,它是指令的有限序列,其中每一条指令表示一个或多个操作,一个算法还具有下列 5 5 个重要特性:
- 有穷性:一个算法必须总是(对任何合法的输入值)在执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中的每一条指令必须有确切的含义,理解时不会产生二义性。并且在任何条件下,算法只有唯一的一条执行路径,即对于相同的输入只能得出相同的输出。
- 可行性:一个算法是可行的,即算法中描述的操作都可以通过已经实现的基本运算执
行有限次来实现。 - 输入:一个算法有零个或多个输入,这些输入取自于某个特定的对象的集合。
- 输出:一个算法有一个或多个输出,这些输出是同输入有着某些特定关系的量。
2. 算法设计
一个好的算法应考虑多个目标,包括正确性、可读性、健壮性和高效性等。
存在多种算法设计技术(也称为算法设计策略),它们是设计算法的一般性方法。算法设计技术主要有分治法、动态规划法、贪心法、回溯法、分支限界法,概率算法和近似算法等。
3. 算法分析
指对一个算法所需要的资源进行估算,这些资源包括内存、通信带宽、计算机硬件和时间等,所需要的资源越多,该算法的复杂度就越高。
对于任何给定的问题,设计出复杂度尽可能低的算法是设计算法时追求的重要目标;另一方面,当给定问题有很多种算法时,选择其中复杂度最低者是一个重要准则。因此,选择算法标准:正确性、可靠性、简单性、易理解性。
在计算机资源中,最重要的是时间和空间(存储器)资源,因此复杂度分析主要包括时间复杂度和空间复杂度分析。
4. 算法的表示
- 自然语言:优点【容易理解】,缺点【容易出现二义性,并且算法通常很冗长】。
- 流程图:优点【直观易懂】,缺点【严密性不如程序设计语言,灵活性不如自然语言】。
- 程序设计语言:优点【能用计算机直接执行】,缺点【抽象性差,使算法设计者拘泥于描述算法的具体细节】。
- 伪代码:是介于自然语言和程序设计语言之间的方法,它采用某一程序设计语言的基本语法,同时结合自然语言来表达。
二、 算法分析基础
1. 时间复杂度
指程序运行从开始到结束所需要的时间。通常分析时间复杂度的方法是从算法中选取一种对于所研究的问题来说是基本运算的操作以该操作重复执行的次数作为算法的时间度量。
即使对于相同的输入规模,数据分布不相同也影响了算法执行路径的不同,因此所需要的执行时间也不同。根据不同的输入,将算法的时间复杂度分析分为
3 3 种情况:
- 最佳情况:使算法执行时间最少的输入,一般情况下,不进行算法在最佳情况下的时间复杂度分析。
- 最坏情况:使算法执行时间最多的输入,一般会进行算法在最坏时间复杂度的分析。
- 平均情况:算法的平均运行时间,一般来说,这种情况很难分析,平均情况分析可以按:将所有的输入按其执行时间分类;确定每类输入发生的概率;确定每类输入的执行时间步骤进行。
2. 空间复杂度
指对一个算法在运行过程中临时占用存储空间大小的度量。一个算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小。
2. 渐进符号
一般来说,算法中原操作重复执行的次数是规模 n n 的某个函数 T ( n ) T(n) 。由于许多情况下要精确计算 T ( n ) T(n) 是困难的,因此引入了渐进时间复杂度在数量上估计一个算法的执行时间。
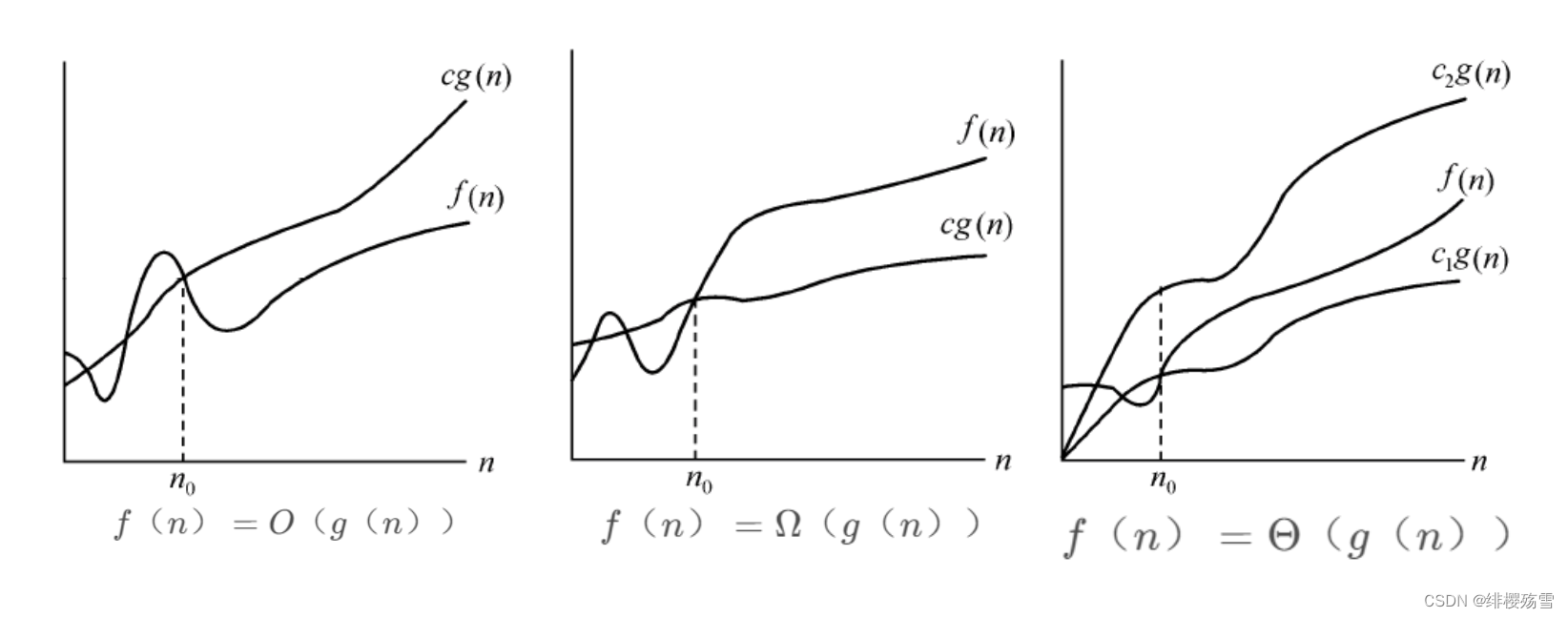
- O O 记号: O ( g ( n )) = { f ( n ) O(g(n))= \ f(n) 存在正常数 c c 和 n 0 n_0 ,使得对所有的 n ≥ n 0 n ≥ n_0 ,有 0 ≤ f ( n ) ≤ c g ( n ) } , O ( g ( n )) 0 ≤ f(n)≤ cg(n)\,O(g(n)) 表示一个函数集合,往往用该记号给出一个算法运行时间的渐进上界。
- Ω Ω 记号: Ω ( g ( n )) = { f ( n ) Ω(g(n))= \ f(n) 存在正常数 c c 和 n 0 n_0 ,使得对所有的 n ≥ n 0 n ≥ n_0 ,有 0 ≤ c g ( n ) ≤ f ( n ) } , Ω ( g ( n )) 0 ≤ cg(n)≤ f(n)\,Ω(g(n)) 表示一个函数集合,往往用该记号给出一个算法运行时间的渐进下界。
-
θ θ
记号:
Θ ( g ( n )) = { f ( n ) Θ(g(n))= \ f(n)
存在正常数
c 1 、 c 2 c_1、c_2 和
n 0 n_0 ,使使得对所有的
n ≥ n 0 n ≥ n_0 ,有
0 ≤ c 1 g ( n ) ≤ f ( n ) ≤ c 2 g ( n ) } , Θ ( g ( n )) 0
≤ c_1g(n)≤ f(n) ≤ c_2g(n)\,Θ(g(n))
表示一个函数集合,往往用该记号给出一个算法运行时间的渐进上界和渐进下界,即渐进紧致界。
常见的对算法执行所需时间的度量: 0 ( 1 ) < O ( l o g 2 n ) < O ( n ) < O ( n l o g 2 n ) < O ( n 2 ) < O ( n 3 ) < O ( 2 n ) 0(1)< O(log_2 n)< O(n)< O(n log_2 n)< O(n^2)< O(n^3)<O (2^n)
3. 递归式
- 展开法
将递归式中等式右边的项根据递归式进行替换,称为展开。展开后的项被再次展开,如此下去,直到得到一个求和表达式,得到结果。 - 代换法
先猜测一个较小值,再用数学归纳法证明猜测的正确性,这种方法比较难用。在用代换法解递归式时需要3个步骤:猜测解的形式;用数学归纳法证明猜测的正确性;求出使解真正有效的常数。 - 递归树法
弥补了代换法猜测困难的缺点,它适于提供“好”的猜测,然后用代换法证明。在递归树中,每一个结点都代表递归函数调用集合中一个子问题的代价。将树中每一层内结点的代价相加得到一个每层代价的集合,再将每层的代价相加得到递归式所有层的总代价。当用递归式表示分治算法的时间复杂度时,递归树方法尤其有用。 - 主方法
也称为主定理,给出了求解以下形式的递归式的快速方法。 T ( n ) = a T ( n / b ) + f ( n ) T(n)=aT(n/b)+f(n)
其中, a ≥ 1 a ≥ 1 和 b > 1 b > 1 是常数, f ( n ) f(n) 是一个渐进的正函数。
设 a ≥ 1 a ≥ 1 和 b > 1 b > 1 为常数, f ( n ) f(n) 为函数, T ( n ) T(n) 为定义在非负整数上的递归式, T ( n ) = a T ( n / b ) + f ( n ) T(n) = aT(n / b)+ f(n) ,其中, n / b n / b 指 ⌊ n / b ⌋ \lfloor n / b \rfloor 或 ⌈ n / b ⌉ \lceil n / b \rceil ,那么 T ( n ) T(n) 可能有如下的渐进紧致界:
① 若对于某常数 ε > 0 ε > 0 ,有 f ( n ) = O ( n l o g b a − ε ) f(n)= O(n^{log_ba - ε}) ,则 T ( n ) = Θ ( n l o g b a ) T(n)= Θ(n^{log_ba})
② 若 f ( n ) = Θ ( n l o g b a l o g k n ) f(n)= Θ(n^{log_ba} log^k n) ,则 T ( n ) = Θ ( n l o g b a l o g k + 1 n ) T(n)= Θ(n^{log_ba} log^{k +1 } n)
③ 若对于某常数 ε > 0 ε > 0 ,有 f ( n ) = O ( n l o g b a + ε ) f(n)= O(n^{log_ba + ε}) ,且对于常数 c < 1 c < 1 与所有足够大的 n n 有 a f ( ( b / n ) ≤ c f ( n ) af((b/n)≤ cf(n) ,则 T ( n ) = Θ ( f ( n )) T(n)= Θ(f(n)) 。
三、 分治法
1. 递归的概
递归 = 递推 +
回溯,指子程序(或函数)直接调用自己或通过一系列调用语句间接调用自己,是一种描述问题和解决问题的常用方法。
两个基本要素:边界条件【即确定递归到何时终止,也称为递归出口】;递归模式【即大问题是如何分解为小问题的,也称为递归体】。
2. 分治法的基本思想概念
分治和递归就像孪生兄弟。分治法的思想是将一个难以直接解决的大问题分解成一些规模较小的相同问题,这些问题互相独立,分而治之。一般来说,分治算法在每一层递归上都有三个步骤:
① 分解:将原问题分解成一系列子问题。
② 求解:递归地求解各子问题。若子问题足够小,则直接求解。
③ 合并:将子问题的解合并成原问题的解。
- 使用场景
① 该问题的规模缩小到一定的程度就可以容易地解决
② 利用该问题分解出的子问题的解可以合并为该问题的解
③ 该问题所分解出的各个子问题是相互独立的
3. 分治法的典型实例
(1)最大子段和问题
最大子段和问题的分治策略如下:

// C 语言:
#include <stdio.h>
// 返回两个数中较大的值
int max(int a, int b) {
return (a > b) ? a : b;
}
// 返回三个数中的最大值
int max3(int a, int b, int c) {
return max(max(a, b), c);
}
// 返回连续子数组的最大和
int maxSubarraySum(int arr[], int size) {
int maxSoFar = arr[0]; // 当前最大子段和
int maxEndingHere = arr[0]; // 包含当前元素的最大子段和
for (int i = 1; i < size; i++) { // 遍历数组,更新最大子段和
maxEndingHere = max(arr[i], maxEndingHere + arr[i]);
maxSoFar = max(maxSoFar, maxEndingHere);
}
return maxSoFar;
}
int main(void) {
int arr[] = {-2, -6, 4, 12, -2, 1, 8, -10};
int size = sizeof(arr) / sizeof(arr[0]);
int maxSum = maxSubarraySum(arr, size);
printf("最大子段和为: %d\n", maxSum);
return 0;
}
四、 动态规划法
1. 动态规划法的基本思想
与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合用动态规划法求解的问题,经分解得到的子问题往往不是独立的,不同子问题的数目常常只有多项式量级。如果能够保存已解决的子问题的答案,在需要时再找出已求得的答案,这样就可以避免大量的重复计算,从而得到多项式时间的算法。为了达到这个目的,可以用一个表来记录所有已解决的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。
动态规划算法通常用于求解具有某种最优性质的问题。设计一个动态规划算法,步骤如下:
① 确定问题的阶段:将原问题划分为若干个阶段,每个阶段对应一个决策点。
② 定义状态:确定每个阶段的状态,状态是原问题中需要记录的关键信息。
③
确定状态转移方程:根据问题的性质和阶段的状态定义,建立各个阶段之间的状态转移关系。
④ 确定边界条件:确定问题的边界情况,即最简单的情况下的解。
⑤ 确定目标函数:根据问题的要求,确定需要优化的目标函数。
⑥
建立递推关系:根据状态转移方程,利用已知的子问题最优解逐步推导出当前阶段的最优解。
⑦
求解问题:根据递推关系,自底向上地求解各个阶段的最优解,直到得到原问题的最优解。找出最优解的性质,并刻画其结构特征。
2. 动态规划法的典型实例
(1)0- 1 背包问题
动态规划 0-1 背包问题步骤如下:

// C 语言:
#include <stdio.h>
// 返回两个数中较大的值
int max(int a, int b) {
return (a > b) ? a : b;
}
// 返回 0-1 背包问题的最大价值
int knapSack(int W, int weight[], int value[], int n) {
int dp[n + 1][W + 1];
for (int i = 0; i <= n; i++) { // 初始化数组
for (int w = 0; w <= W; w++) {
if (i == 0 || w == 0)
dp[i][w] = 0;
else if (weight[i - 1] <= w)
dp[i][w] = max(value[i - 1] + dp[i - 1][w - weight[i - 1]], dp[i - 1][w]);
else
dp[i][w] = dp[i - 1][w];
}
}
return dp[n][W];
}
int main(void) {
int value[] = {60, 100, 120};
int weight[] = {10, 20, 30};
int W = 50;
int n = sizeof(value) / sizeof(value[0]);
int maxValue = knapSack(W, weight, value, n);
printf("0-1背包问题的最大价值为: %d\n", maxValue);
return 0;
}
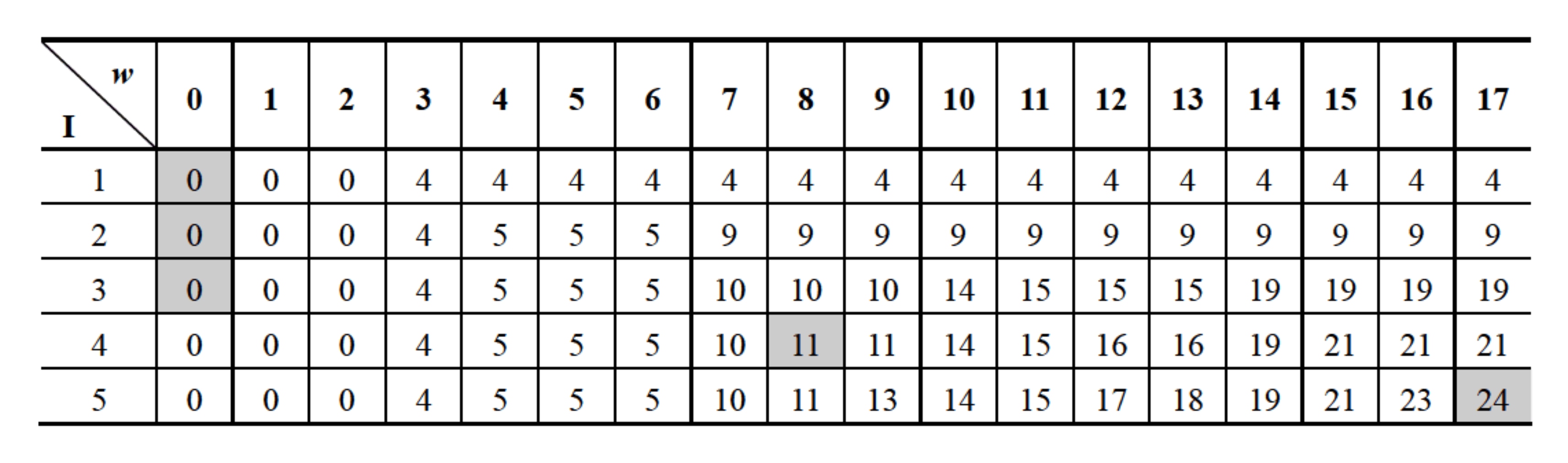
有 n n 个物品,第 i i 个物品价值为 v i v_i ,重量为 w i w_i ,其中 v i v_i 和 w i w_i 均为非负数,背包的容量为 W W , W W 为非负数,每个物品的价值和重量如下表所示,假设: n = 5 , W = 17 n = 5,W = 17 ,求现如何选择装入背包的物品,使装入背包的物品总价值最大?
目标函数为: m a x ∑ i = 1 n v i x i max \sum_{i = 1}^n v_i x_i ,约束条件为: ∑ i = 1 n w i x i ≤ W , x i ∈ { 0 , 1 } \sum_{i = 1}^n w_i x_i ≤ W,x_i ∈ \0,1\ ,填表。
从上表中可以很容易地看出最优解的值为: 24 24 。构造最优解的时间复杂度为: 【 O ( n )】 【O(n)】 , C [ 5 , 17 ] = 24 ≠ C [ 4 , 17 ] = 21 , x 5 = 1 ; C [ 4 , 8 ] = 11 ≠ C [ 3 , 8 ] = 10 , x 4 = 1 ; C [ 2 , 0 ] = C [ 2 , 0 ] = C [ 1 , 0 ] = 0 , x 3 = x 2 = x 1 = 0 C[5,17] = 24 ≠ C[4,17] = 21,x_5=1;C[4,8] = 11 ≠ C[3,8] = 10,x_4 = 1;C[2,0] = C[2,0] = C[1,0] = 0,x_3 = x_2 = x_1 = 0 ,因此最优解为: ( 0 , 0 , 0 , 1 , 1 ) (0,0,0,1,1) 。
(2) 最长公共子序列(LCS)
给定两个序列
X X 和
Y Y ,称序列
Z Z 是
X X 和
Y Y 的公共子序列,是指
Z Z 同时是
X X 和
Y Y 的子序列。最长公共子序列问题定义为:给定序列
X = x 1 x 2 … x m X = x_1x_2…x_m 和序列
Y = y 1 y 2 … y n Y=y_1y_2…y_n
,求这两个序列的最长公共子序列。
动态规划 最长公共子序列(LCS)问题步骤如下:

// C 语言:
#include <stdio.h>
#include <string.h>
// 返回两个数中的较大值
int max(int a, int b) {
return (a > b) ? a : b;
}
// 计算最长公共子序列的长度
int lcs(char *X, char *Y, int m, int n) {
int L[m + 1][n + 1]; // 创建一个二维数组来存储子问题的解
int i, j;
for (i = 0; i <= m; i++) { // 填充 L[][] 数组,从底部开始逐步构建
for (j = 0; j <= n; j++) {
if (i == 0 || j == 0)
L[i][j] = 0; // 如果其中一个字符串为空,最长公共子序列的长度为 0
else if (X[i - 1] == Y[j - 1])
L[i][j] = L[i - 1][j - 1] + 1; // 如果末尾字符相同,LCS 长度加 1
else
L[i][j] = max(L[i - 1][j], L[i][j - 1]); // 否则取左边或上边的最大值
}
}
return L[m][n]; // 返回右下角的值,即整个问题的解
}
int main(void) {
char X[] = "AGGTAB";
char Y[] = "GXTXAYB";
int m = strlen(X);
int n = strlen(Y);
printf("最长公共子序列为:%d\n", lcs(X, Y, m, n)); // 打印最长公共子序列的长度
return 0;
}
五、 贪心法
1. 贪心法的基本思想
是一种简单的方法。和动态规划法一样,贪心法也经常用于解决最优化问题。与动态规划法不同的是,贪心法在解决问题的策略上是仅根据当前已有的信息做出选择,而且一旦做出了选择,不管将来有什么结果,这个选择都不会改变。采用贪心法的两个性质:
- 最优子结构
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构。问题具有最优子结构是该问题可以采用动态规划法或者贪心法求解的关键性质。 - 贪心选择性质
指问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来得到。这是贪心法和动态规划法的主要区别。证明一个问题具有贪心选择性质也是贪心法的一个难点。
2. 贪心法的典型实例
(1)背包问题
有 n n 个物品,第 i i 个物品价值为 v i v_i ,重量为 w i w_i ,其中 v i v_i 和 w i w_i 均为非负数,背包的容量为 W W , W W 为非负数,每个物品的价值和重量如下表所示,假设: n = 5 , W = 100 n = 5,W = 100 ,求现如何选择装入背包的物品,使装入背包的物品总价值最大?
① 按最大价值先放背包的原则:先放物品 1 1 和 4 4 ,获得价值: 65 + 60 = 125 65 + 60 = 125 ,背包还剩容量: 100 − 30 − 50 = 20 100 - 30 - 50 = 20 ,此时物品 5 5 是价值最大的,但其重量为 40 40 ,不能全部放入背包。而且一般将物品 2 2 和 3 3 放入背包比把物品 5 5 的一半放入背包能获得更大的价值。因此把物品 2 2 放入背包,得到价值: 125 + 20 = 145 125 + 20 = 145 ,剩余容量: 20 − 10 = 10 20 - 10 = 10 。此时可再放入物品 3 3 的 1 3 \frac{1}{3} ,得到总价值: 145 + 1.5 × 10 = 160 145 + 1.5 × 10 = 160 ,对应的解为: { 1 , 1 , 1 3 , 1 , 0 } \1,1,\frac{1}{3},1,0\ 。
② 最小重量先放背包的原则:将物品 2 、 3 、 1 2、3、1 和 5 5 放入背包中,刚好装满,得到价值 20 + 30 + 65 + 40 = 155 20 + 30 + 65 + 40 = 155 ,对应的解为: { 1 , 1 , 1 , 0 , 1 } \1,1,1,0,1\
③ 按最大单位重量价值先放背包的原则:将物品 1 、 2 1、2 和 3 3 放入背包中,得到价值: 65 + 20 + 30 = 115 65 + 20 + 30 = 115 ,剩余容量: 100 − 30 − 10 − 20 = 40 100 - 30 - 10 - 20 = 40 。此时可再放入物品 4 4 的 4 5 \frac{4}{5} ,得到总价值: 115 + 4 5 × 60 = 163 115 + \frac{4}{5} × 60 = 163 ,对应的解为: { 1 , 1 , 1 , 4 5 , 0 } \1,1,1,\frac{4}{5},0\ 。
可以证明,③ 为问题的最优解,因此用贪心法求解背包问题,应根据该原则来放置物品。
六、 回溯法
以深度优先的方式系统地搜索问题的解的方法称为回溯法,它适用于解一些组合数较大的问题。有"通用的解题法"之称,是一个既带有系统性又带有跳跃性的搜索算法,用它可以系统地搜索一个问题的所有解或任一解。
过程:它在包含问题的所有解的解空间树中,按照深度优先的策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时,总是先判断该结点是否肯定不包含问题的解。如果肯定不包含,则跳过对以该结点为根的子树的系统搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先的策略进行搜索。
回溯法在用来求问题的所有解时要回溯到根,且根结点的所有子树都已被搜索遍才结束。而用来求问题的任一解时,只要搜索到问题的一个解就可以结束。
1. 回溯法的算法框架
(1)问题的解空间
在应用回溯法解问题时,首先应明确定义问题的解空间。问题的解空间应至少包含问题的一个(最优) 解。定义了问题的解空间后,还应将解空间很好地组织起来,使得用回溯法能方便地搜索整个解空间,通常将解空间表示为树或图的形式。
(2)回溯法的基本思想
在确定了解空间的组织结构后,回溯法从开始结点(根结点)出发,以深度优先的方式搜索整个解空间。这个开始结点就成为一个活结点,同时也成为当前的扩展结点。在当前的扩展结点处,搜索向纵深方向移至一个新结点。这个新结点就成为一个新的活结点,并成为当前扩展结点。如果在当前扩展结点处不能再向纵深方向移动,则当前的扩展结点就成为死结点。此时,应往回移动(回溯)至最近的一个活结点处,并使这个活结点成为当前的扩展结点。回溯法即以这种工作方式递归地在解空间中搜索,直到找到所要求的解或解空间中已无活结点时为止。运用回溯法解题步骤如下:
① 确定问题的状态空间:确定问题的解空间,包括可能的候选解和约束条件。
②
定义可行解:根据约束条件确定可行解的定义,即确定那些候选解是符合条件的。
③
构建候选解:根据当前状态,生成一个或多个候选解,即在可行解的范围内进行搜索。
④ 搜索:对每个生成的候选解进行搜索,判断其是否符合条件。
⑤
判断是否成功:如果当前候选解符合条件,则保存结果并继续搜索下一个状态;否则,回溯到上一个状态,重新选择候选解。
⑥
剪枝:在搜索过程中,根据问题的性质和约束条件,及时剪枝,避免不必要的计算。
⑦ 输出结果:当所有状态都搜索完毕后,输出所有符合条件的候选解。
(3)回溯法的算法框架
回溯法的算法框架有非递归和递归两种方式。
(4) 回溯法的限界函数
限界函数的设计是回溯法的一个核心问题,也是一个很难的问题。
指导原则:尽可能多和尽可能早地“杀掉"不可能产生最优解的活结点。好的限界函数可以大大减少问题的搜索空间,从而大大提高算法的效率。
2. 回溯法的典型实例
(1)0- 1 背包问题
有 n n 个物品,第 i i 个物品价值为 v i v_i ,重量为 w i w_i ,其中 v i v_i 和 w i w_i 均为非负数,背包的容量为 W W , W W 为非负数,每个物品的价值和重量如下表所示,假设: n = 8 , W = 110 n = 8,W = 110 ,求现如何选择装入背包的物品,使装入背包的物品总价值最大?
> 根据上图树中的结点内若有数据,则上面表示背包当前的重量,下面表示背包当前的价值;结点内若无数据,则旁边的数据表示在现有的选择下背包能获得的价值的上界。 X ( i ) = 1 X(i)= 1 和 X ( i ) = 0 X(i)= 0 分别表示第 i i 个物品放入和不放入背包中。浅灰色结点表示对应可行解的值,存在 5 5 个可行解,其值分别为 139 、 149 、 151 、 96 、 159 139、149、151、96、159 ,对应的解分别为: X 1 = ( 1 , 1 , 1 , 1 , 1 , 0 , 0 , 0 )、 X 2 = ( 1 , 1 , 1 , 1 , 0 , 1 , 0 , 0 )、 X 3 = ( 1 , 1 , 1 , 1 , 0 , 0 , 1 , 0 )、 X 4 = ( 1 , 1 , 1 , 1 , 0 , 0 , 0 , 0 )、 X 5 = ( 1 , 1 , 1 , 0 , 1 , 1 , 0 , 0 ) X_1 =(1,1,1,1,1,0,0,0)、X_2 =(1,1,1,1,0,1,0,0)、X_3 =(1,1,1,1,0,0,1,0)、X_4 =(1,1,1,1,0,0,0,0)、X_5 =(1,1,1,0,1,1,0,0) 。其中, X 5 X_5 为最优解,其值为: 159 159 。
(2) n 皇后问题
问题要求:在一个
n × n n × n 格的棋盘上放置
n n
个皇后,使得它们彼此不受攻击。按照国际象棋的规则,一个皇后可以攻击与之处在同一行或同一列或同一条斜线上的其他任何棋子。因此,
n n 皇后问题等价于要求在一个
n × n n × n 格的棋盘上放置
n × n n × n
,使得任何两个皇后不能被放在同一行或同一列或同一条斜线上。
求解过程:从空棋盘开始,设在第
1 1 行至第
m m 行都已经正确地放置了
m m 个皇后,再在第
m + 1 m + 1 行上找合适的位置放第
m + 1 m + 1 皇后,直到在第
n n 行也找到合适的位置放置第
n n 个皇后,就找到了一个解。接着改变第
n n
行上皇后的位置,希望获得下一个解。另外,在任一行上有
n n 种可选的位置。开始时,位置在第
1 1 列,以后改变时,顺次选择第
2 2 列、第
3 3 列、…、第
n n 列。当第
n n
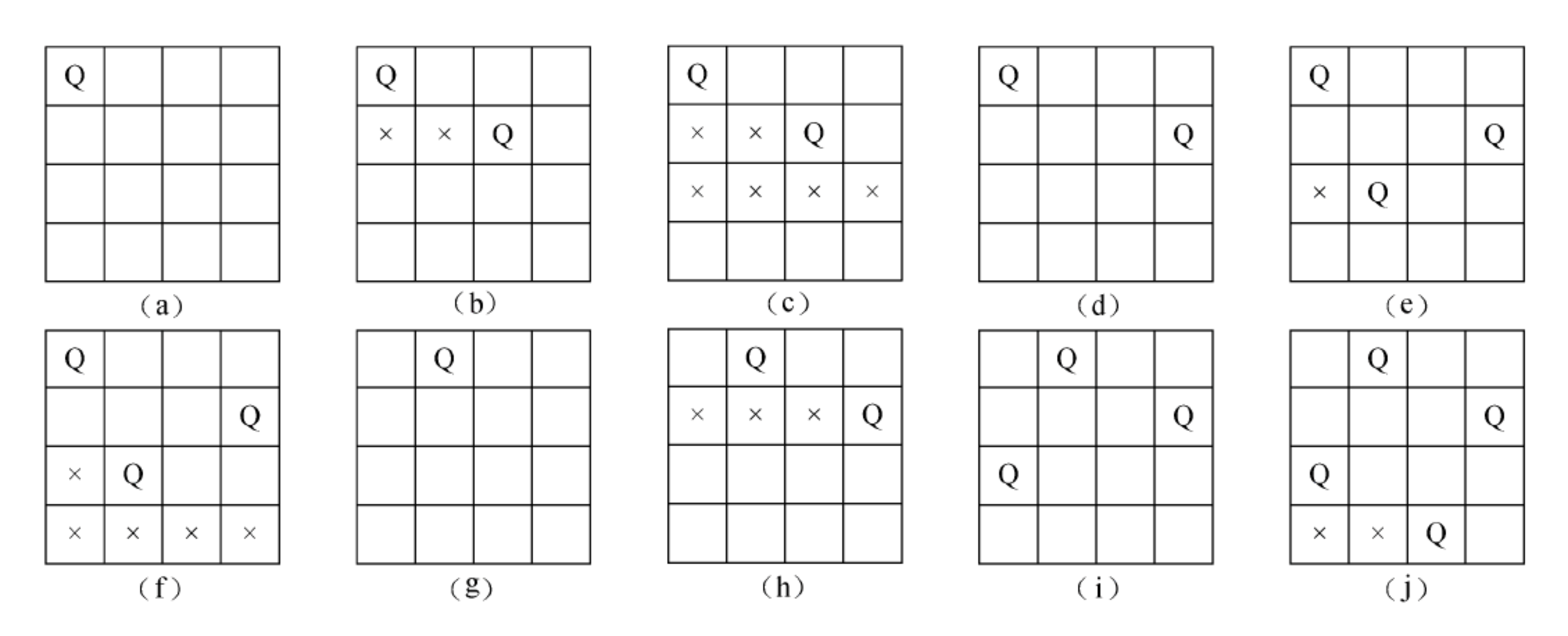
列也不是一个合理的位置时,就要回溯,去改变前一行的位置。回溯法求解
4 − 4- 皇后问题的搜索过程如下图:
七、 分支限界法
分支限界法类似于回溯法,也是一种在问题的解空间树 T T 上搜索问题解的算法。但在一般情况下,分支限界法与回溯法的求解目标不同。
| 回溯法 | 分支限界法 | |
|---|---|---|
| 求解目标 | 找出T中满足约束条件的所有解 | 找出满足约束条件的最优解 |
| 搜索方式 | 深度优先 | 广度优先或最小耗费优先 |
| 搜索策略 | 可以回溯 | 每一个活结点只有一次机会成为扩展结点 |
| 核心问题(相同1) | 限界函数的设计 | 限界函数的设计 |
如何设计限界函数来有效地减小搜索空间是应用分支限界法要考虑的问题,根据从活结点表中选择下一扩展结点的不同方式,可将分支限界法分为几种不同的类型,最常用的有以下两种:
- 队列式(FIFO,先进先出)分支限界法
队列式分支限界法将活结点表组织成一个队列,并按队列的先进先出原则选择下一个结点作为扩展结点。 - 优先队列式分支限界法
优先队列式分支限界法将活结点表组织成一个优先队列,并按优先队列中规定的结点优先级选取优先级最高的下一个结点作为扩展结点。
优先队列中规定的结点优先级通常用一个与该结点相关的数值 p p 来表示。结点优先级的高低与 p p 值的大小相关。
(1)0- 1 背包问题
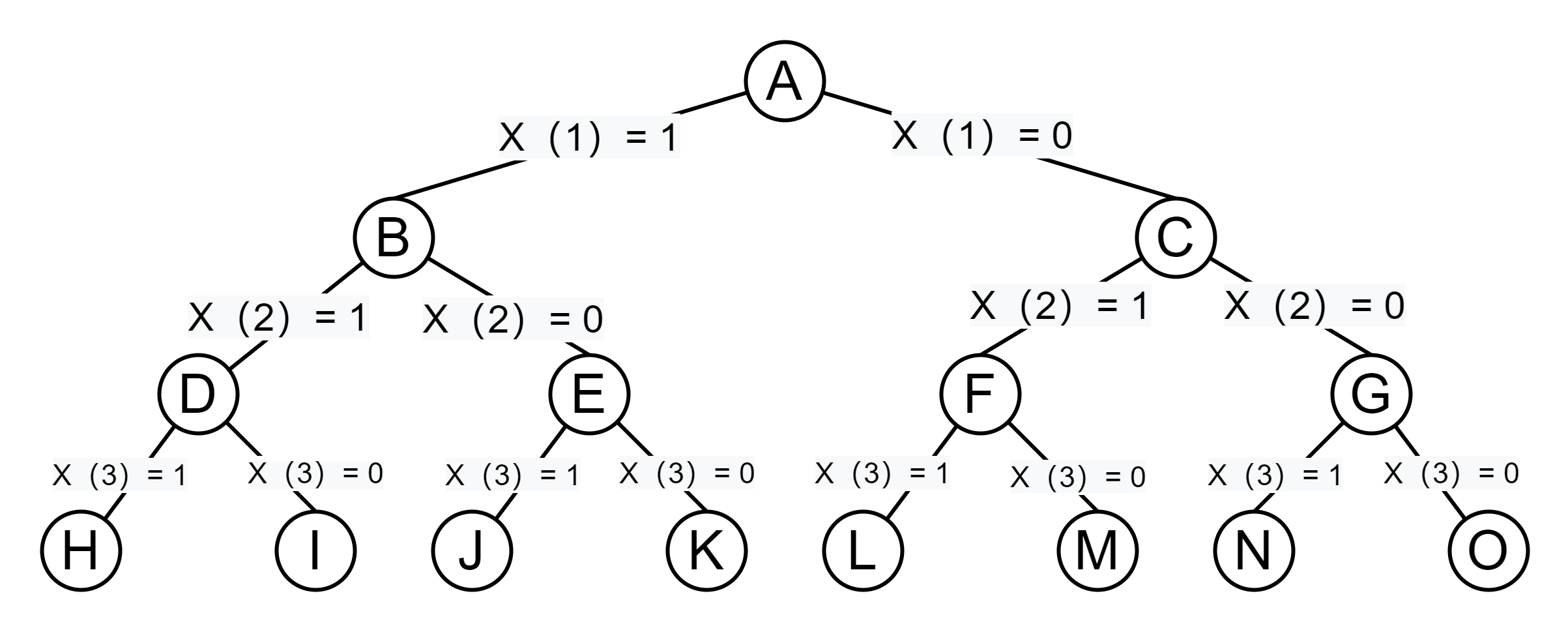
n = 3 n = 3 时 0 − 1 0-1 背包问题的一个实例: w = [ 16 , 15 , 15 ] , p = [ 45 , 25 , 25 ] , c = 30 w = [16,15,15],p = [45,25,25],c = 30 。其解空间树如下所示:
用队列式分支限界法解此问题时,用一个队列来存储活结点表。算法从根结点 A A 出发。
① 初始时活结点队列为空。
② 结点 A A 是当前扩展结点,它的两个儿子结点 B B 和 C C 均为可行结点,故将这两个儿子结点按照从左到右的顺序加入活结点队列,并且舍弃当前扩展结点 A A 。
③ 按照先进先出的原则,下一个扩展结点是活结点队列的队首结点 B B 。扩展结点 B B 得到其儿子结点 D D 和 E E 。由于 D D 是不可行结点,故被舍去。 E E 是可行结点,被加入活结点队列。此时活结点队列中的元素是 C C 和 E E 。
④ C C 成为当前扩展结点,它的两个儿子结点 F F 和 G G 均为可行结点,因此被加入活结点队列。此时活结点队列中的元素是 E 、 F 、 G E、F、G 。
⑤ 扩展下一个结点 E E ,得到结点 J J 和 K K 。 J J 是不可行结点,因而被舍去。 K K 是一个可行的叶子结点,表示所求问题的一个可行解,其价值为 45 45 。此时活结点队列中的元素是 F F 和 G G 。
⑥ 当前活结点队列的队首结点 F F 成为下一个扩展结点。它的两个儿子结点 L L 和 M M 均为叶子结点。 L L 表示获得价值为 50 50 的可行解, M M 表示获得价值为 25 25 的可行解。
⑦ G G 是最后一个扩展结点,其儿子结点 N N 和 O O 均为可行叶子结点。最后活结点队列为空,算法终止。算法搜索得到最优解的值为 50 50 ,对应的解为 ( 0 , 1 , 1 ) (0,1,1) 。
八、 概率算法
概率算法的一个基本特征:对所求解问题的同一实例用同一概率算法求解两次,可能得到完全不同的效果。这两次求解所需的时间甚至所得到的结果可能会有相当大的差别。如果一个问题没有有效的确定性算法可以在一个合理的时间内给出解,但是该问题能接受小概率错误,那么采用概率算法就可以快速找到这个问题的解。
一般情况下,概率算法具有以下基本特征:
- 概率算法的输入包括两部分,一部分是原问题的输入,另一部分是一个供算法进行随机选择的随机数序列。
- 概率算法在运行过程中,包括一处或多处随机选择,根据随机值来决定算法的运行路径。
- 概率算法的结果不能保证一定是正确的,但能限制其出错概率。
- 概率算法在不同的运行过程中,对于相同的输入实例可以有不同的结果,因此,对于相同的输入实例,概率算法的执行时间可能不同。
概率算法大致分为四类:
- 数值概率算法:常用于数值问题的求解,这类算法得到的往往是近似解,且近似解的精度随计算时间的增加不断提高。
- 蒙特卡罗(Monte Carlo)算法:用于求问题的精确解。
- 拉斯维加斯(LasVegas)算法:不会得到不正确的解。
- 舍伍德(Sherwood)算法:总能求得问题的一个解,且所求得的解总是正确的。
九、 近似算法
是解决难解问题的一种有效策略。
基本思想:放弃求最优解,而用近似最优解代替最优解,以换取算法设计上的简化和时间复杂度的降低。
过程:虽然它可能找不到一个最优解,但它总会给待求解的问题提供一个解。为了具有实用性,近似算法必须能够给出算法所产生的解与最优解之间的差别或者比例的一个界限,它保证任意一个实例的近似最优解与最优解之间相差的程度。显然,这个差别越小,近似算法越具有实用性。
衡量近似算法性能的标准:
- 算法的时间复杂度:近似算法的时间复杂度必须是多项式阶的,这是近似算法的
基本目标。 - 解的近似程度:近似最优解的近似程度也是设计近似算法的
重要目标。近似程度与近似算法本身、问题规模,乃至不同的输入实例有关。
十、 数据挖掘算法
1. 数据挖掘概述
数据挖掘的核心是算法,其主要功能包括分类、回归、关联规则和聚类等。
数据挖掘利用机器学习方法对多种数据,包括数据库数据、数据仓库数据、Web数据等进行分析和挖掘。
2. 分类
分类是一种有监督的学习过程,根据历史数据预测未来数据的模型。分类的数据对象属性分为:一般属性和分类属性或者目标属性。
对数据分类有两个步骤:学习模型【指基于训练数据集采用分类算法建立学习模型】和应用模型【指应用测试数据集的数据到学习模型中,根据输出来评估模型的好坏以及将未知数据输入到学习模型中,预测数据的类型】。
存在多种分类算法:决策树归纳【一种自顶向下的递归树算法】,
I 3 、 C 4.5 I3、C4.5 和
C A R T CART
【典型的决策树算法】,朴素贝叶斯算法和贝叶斯信念网络【基于后验概率的贝叶斯公式进行分类】,后向传播(BP)算法【使用梯度下降法的神经网络方法】,支持向量机(SVM)【用于线性和非线性数据的分类算法】。
3. 频繁模式和关联规则挖掘
挖掘海量数据中的频繁模式和关联规则可以有效地指导企业发现交叉销售机会、进行决策分析和商务管理等。
4. 聚类
是一种无监督学习过程。根据数据的特征,将相似的数据对象归为一类,不相似的数据对象归到不同的类中,这就是聚类,每个聚类也称为簇。
聚类的典型算法有:基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法和基于统计模型的方法。
| 说明 | j经典算法 | |
|---|---|---|
| 基于划分的方法 | 基于划分的方法将 n n 个数据对象划分为 k k 个不相交的集合,每个集合称为一个簇 | k-均值、k-中心点算法… |
| 基于层次的方法 | 将数据对象集进行层次的分解,根据其是自底向上还是自顶向下分解,可以分为凝聚的方法和分裂的方法 | AGNES、DIANA |
| 基于密度的方法 | 基于数据对象的邻域来进行聚类分析,因此可以识别各种形状的簇,以及一个数据对象可以属于多个不同的簇 | DBSCAN、OPTICS 和 DENCLUE |
| 基于网格的方法 | 把对象空间量化为有限个单元,形成一个网格结构 | STING、CLIQUE |
| 基于统计模型的方法 | 将数据对象集看作多个服从不同分布的数据集构成,聚类的目的是识别出这些不同的分布的数据对象 | EM |
十一、 智能优化算法
1. 智能优化算法概述
优化技术:一种以数学为基础,用于求解各种工程问题优化解的应用技术。
智能优化算法包括:人工神经网络(ANN)、混沌、遗传算法、进化规划、模拟退火(SA)、禁忌搜索(TA)及其混合优化策略等。
2. 人工神经网络(ANN)
是一个以有向图为拓扑结构的动态系统,它通过对连续或断续的输入作状态响应而进行信息处理。人工神经网络技术与计算机技术的结合,为人类进一步研究模拟人类智能及了解人脑思维的奥秘开辟了一条新途径。
3. 遗传算法
是建立在自然选择和群体遗传学基础上,通过自然选择、杂交和变异实现搜索的方法。
4. 模拟退火(SA)算法
是一种求解全局优化算法。模拟退火算法的基本思想来源于物理退火过程、所谓物理退火过程包括三个阶段:加温阶段、等温阶段、冷却阶段。
5. 禁忌搜索(TA)算法
是模拟人类智力过程的一种全局搜索算法,是对局部邻域搜索的一种扩展。
6. 蚁群算法
蚁群算法的原理:蚂蚁在寻找食物或者寻找回巢的路径中,会在它们经过的地方留下一些信息素,而信息素能被同一蚁群中后来的蚂蚁感受到,并作为一种信号影响后到者的行动,而后到者留下的信息素会对原有的信息素进行加强,并如此循环下去。这样,经过蚂蚁越多的路径,在后到蚂蚁的选择中被选中的可能性就越大。由于在一定的时间内,越短的路径会被越多的蚂蚁访问,因而积累的信息素也就越多,在下一个时间内被其他的蚂蚁选中的可能性也就越大。这个过程会一直持续到所有的蚂蚁都走最短的那一条路径为止。这种行为表现出一种信息正反馈现象:某一路径上走过的蚂蚁越多,则后到者选择该路径的概率就越大,因此距离近的食物源会吸引越来越多的蚂蚁,信息素浓度的增长速度就会越快,同时通过这种信息的交流,蚂蚁也就寻找到食物与蚁穴之间的最短路径了。
7. 粒子群优化算(PSO)
粒子群算法的基本思想:鸟群觅食飞行时,在飞行过程中经常会突然改变方向、散开、聚集,其行为不可预测,但其整体总保持一致性,个体与个体间也保持着最适宜的距离。通过对类似生物群体行为的研究,发现生物群体中存在着一种信息共享机制,为群体的进化提供了一种优势,这就是基本粒子群算法形成的基础。